��Ŀ����
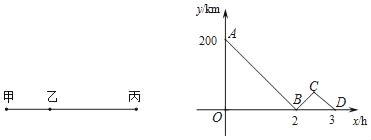
����Ŀ��ij����������һ�ֲ�Ʒ,���ֲ�Ʒ�ijɱ���Ϊ10Ԫ/ǧ��,��֪���ۼ۲����ڳɱ���,����۲��Ź涨���ֲ�Ʒ�����ۼ۲�����18Ԫ/ǧ��,�г����鷢��,�ò�Ʒÿ���������y(ǧ��)�����ۼ�x(Ԫ/ǧ��)֮��ĺ�����ϵ��ͼ��ʾ:
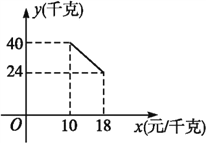
��1����y��x֮��ĺ�����ϵʽ,��д���Ա���x��ȡֵ��Χ;
��2����ÿ�����������W(Ԫ)�����ۼ�x(Ԫ/ǧ��)֮��ĺ�����ϵʽ.�����ۼ�Ϊ����ʱ,ÿ��������������?��������Ƕ���?
��3���þ�������Ҫÿ����168Ԫ����������,���ۼ�Ӧ��Ϊ����?
���𰸡���1��y��x֮��ĺ�����ϵʽy=-2x+60(10��x��18)����2�������ۼ�Ϊ18Ԫʱ,ÿ��������������,���������192Ԫ����3���þ�������Ҫÿ����168Ԫ����������,���ۼ�Ӧ��Ϊ16Ԫ.
����������1���������⣬��һ�κ����Ľ���ʽΪy=kx+b������ͼ�е�������֪�ĵ������(10��40)��(18��24)��������Ԫ�����Ԫһ�η�����ó�k��b��ֵ�����ɵó�һ�κ����Ľ���ʽ��
��2���������������һ�������������������Եõ�W����x�ı���ʽ,Ȼ����ݶ��κ�����������⼴��.
��3����168������κ����Ĺ�ϵʽ����һԪ���η��̼��ɣ�ע���Ա���x��ȡֵ��Χ��
��1����y��x֮��ĺ�����ϵʽy=kx+b,��(10,40),(18,24)�����
![]() , ���
, ���![]() ,
,
��y��x֮��ĺ�����ϵʽy=-2x+60(10��x��18);
��2��W=(x-10)(-2x+60)=-2x2+80x-600,
�Գ���x=20,�ڶԳ�������y����x�����������,
��10��x��18,����x=18ʱ,W���,���Ϊ192.
�������ۼ�Ϊ18Ԫʱ,ÿ��������������,���������192Ԫ
��3����168=-2x2+80x-600,
���x1=16,x2=24(��������,��ȥ)
��:�þ�������Ҫÿ����168Ԫ����������,���ۼ�Ӧ��Ϊ16Ԫ.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�