Question

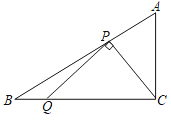
【题目】如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC＝2，点P为AB边上的一个动点，连接PC，过点P作PQ⊥PC交BC边于点Q，则BQ的最大值为_____．

Answer 1

【答案】2

【解析】

过Q作QE⊥AB于E，过C作CF⊥AB于F，利用相似三角形的性质根据一元二次方程，利用根的判别式解决问题即可．

解：过Q作QE⊥AB于E，过C作CF⊥AB于F，

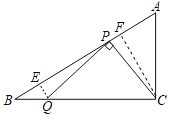
∵在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC＝2，

∴∠B＝30°，

∴AB＝2AC＝4，BC＝AC＝6，

∵∠AFC＝90°，∠A＝60°，

∴∠ACF＝30°，

∴AF＝，CF＝3，

设PF＝x，BQ＝y，

∴QE＝BQ＝y，BE＝y，

∴PE＝3﹣y﹣x，

∵PQ⊥PC，

∴∠PEQ＝∠CFP＝∠CPQ＝90°，

∴∠EQP+∠EPQ＝∠EPQ+∠CPF＝90°，

∴∠PQE＝∠CPF，

∴△PEQ∽△CFP，

∴，

∴

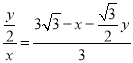
∴x2+（y﹣3）x+＝0，

∵方程有实数解，

∴△≥0，

∴（y﹣3）2﹣6y≥0，

整理得，y2﹣20y+36≥0，

解得y≤2或y≥18（舍弃），

∴BQ≤2，

∴BQ的最大值为2．

故答案为2．