题目内容
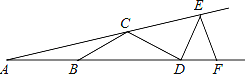
【题目】如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC,AB分别相切于C,D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于M点. 
(1)求证:点M是CF的中点;
(2)若E是 ![]() 的中点,BC=a,写出求AE长的思路.
的中点,BC=a,写出求AE长的思路.
【答案】
(1)解:证明:∵AB与⊙O相切于点D,
∴OD⊥AB于D.
∴∠ODB=90°.
∵CF∥AB,
∴∠OMF=∠ODB=90°.
∴OM⊥CF.
∴点M是CF的中点
(2)解:思路:
连接DC,DF.
①由M为CF的中点,E为 ![]() 的中点,
的中点,
可以证明△DCF是等边三角形,且∠1=30°;
②由BA,BC是⊙O的切线,可证BC=BD=a.
由∠2=60°,从而△BCD为等边三角形;
③在Rt△ABC中,∠B=60°,BC=BD=a,可以求得AD=a,CO= ![]() ,OA=
,OA= ![]() ;
;
④AE=AO﹣OE= ![]() ﹣
﹣ ![]() =
= ![]() .
.
解:连接DC,DF,

由(1)证得M为CF的中点,DM⊥CF,
∴DC=DF,
∵E是 ![]() 的中点,
的中点,
∴CE垂直平分DF,
∴CD=CF,
∴△DCF是等边三角形,
∴∠1=30°,
∵BC,AB分别是⊙O的切线,
∴BC=BD=a,∠ACB=90°,
∴∠2=60°,
∴△BCD是等边三角形,
∴∠B=60°,
∴∠A=30°,
∴OD= ![]() a,AO=
a,AO= ![]() a,
a,
∴AE=AO﹣OE= ![]() a.
a.
【解析】(1)根据切线的性质得到OD⊥AB于D.根据平行线的性质得到∠OMF=∠ODB=90°.由垂径定理即可得到结论;(2)连接DC,DF.由M为CF的中点,E为 ![]() 的中点,可以证明△DCF是等边三角形,根据等边三角形的性质得到∠1=30°;根据切线的性质得到BC=BD=a.推出△BCD为等边三角形;解直角三角形即可得到结论.
的中点,可以证明△DCF是等边三角形,根据等边三角形的性质得到∠1=30°;根据切线的性质得到BC=BD=a.推出△BCD为等边三角形;解直角三角形即可得到结论.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】列方程或方程组解应用题: 在某场CBA比赛中,某位运动员的技术统计如表所示:
技术 | 上场时间(分钟) | 出手投篮(次) | 投中 | 罚球得分(分) | 篮板 | 助攻(次) | 个人总得分(分) |
数据 | 38 | 27 | 11 | 6 | 3 | 4 | 33 |
注:(i)表中出手投篮次数和投中次数均不包括罚球;
(ii)总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,求本场比赛中该运动员投中两分球和三分球各几个.