��Ŀ����
��ˮƽ�ߺ������߽�ƽ��ֳ����ɸ��߳�Ϊ1��С�����θ��ӣ�С�����εĶ����Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ��������ε����ΪS���ö���θ����ϵĸ�������Ϊa���ڲ��ĸ�����Ϊb����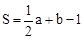 ��ʷ�ơ�Ƥ�˹�ʽ������
��ʷ�ơ�Ƥ�˹�ʽ������
С�������о��ˡ�Ƥ�˹�ʽ�������ܴ������������ǿ��������е������������̽������������������ÿ��С�����������Ϊ1��С�������εĶ���Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ���ͼ�Ǹ��������θ��
�е���������Σ�
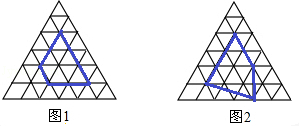
����ͼ���ṩ����Ϣ�����
��S��a��b֮��Ĺ�ϵΪS=�� �����ú�a��b�Ĵ���ʽ��ʾ����
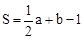 ��ʷ�ơ�Ƥ�˹�ʽ������
��ʷ�ơ�Ƥ�˹�ʽ������С�������о��ˡ�Ƥ�˹�ʽ�������ܴ������������ǿ��������е������������̽������������������ÿ��С�����������Ϊ1��С�������εĶ���Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ���ͼ�Ǹ��������θ��
�е���������Σ�

����ͼ���ṩ����Ϣ�����
| | ������θ����ϵĸ��ĸ��� | ���߶�����ڲ��ĸ����� | ������ε���� |
| �����1 | 8 | 1 | |
| �����2 | 7 | 3 | |
| �� | �� | �� | �� |
| һ�������� | a | b | S |
�⣺������£�
a+2��b��1��
| | ������θ����ϵĸ��ĸ��� | ���߶�����ڲ��ĸ����� | ������ε���� |
| �����1 | 8 | 1 | 8 |
| �����2 | 7 | 3 | 11 |
| �� | �� | �� | �� |
| һ�������� | a | b | S |
�������������8=8+2��1��1����11=7+2��3��1���õ�S=a+2��b��1����

��ϰ��ϵ�д�
�����Ŀ
 ��
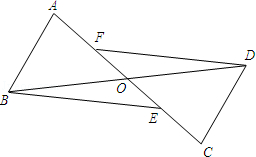
�� ����O�����ĶԳƣ���E��F���߶�AC�ϣ���AF=CE��
����O�����ĶԳƣ���E��F���߶�AC�ϣ���AF=CE��