题目内容
销售甲、乙两种商品所得利润分别为y1(万元)和y2(万元),它们与投入资金u的关系式为y1=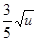 ,y2=
,y2=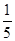 u.如果将3万元资金投入经营甲、乙两种商品,其中对甲商品的投资为x(万元).
u.如果将3万元资金投入经营甲、乙两种商品,其中对甲商品的投资为x(万元).
(1)求经营甲、乙两种商品的总利润y(万元)与x的函数关系式,并直接写出自变量x的取值范围;
(2)设 =t,试写出y关于t的函数关系式,并求出经营甲、乙两种商品各投入多少万元时使得总利润最大.
=t,试写出y关于t的函数关系式,并求出经营甲、乙两种商品各投入多少万元时使得总利润最大.
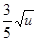 ,y2=
,y2=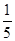 u.如果将3万元资金投入经营甲、乙两种商品,其中对甲商品的投资为x(万元).
u.如果将3万元资金投入经营甲、乙两种商品,其中对甲商品的投资为x(万元).(1)求经营甲、乙两种商品的总利润y(万元)与x的函数关系式,并直接写出自变量x的取值范围;
(2)设
 =t,试写出y关于t的函数关系式,并求出经营甲、乙两种商品各投入多少万元时使得总利润最大.
=t,试写出y关于t的函数关系式,并求出经营甲、乙两种商品各投入多少万元时使得总利润最大.(1)y= +
+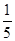 (3-x)(0≤x≤3);(2)甲、乙分别投入
(3-x)(0≤x≤3);(2)甲、乙分别投入 、
、 万元时
万元时
 +
+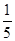 (3-x)(0≤x≤3);(2)甲、乙分别投入
(3-x)(0≤x≤3);(2)甲、乙分别投入 、
、 万元时
万元时试题分析:(1)对甲种商品投资x(万元),对乙种商品投资(3-x)(万元),根据经验公式可得甲、乙两种商品的总利润y(万元)关于x的函数表达式;
(2)利用配方法确定函数的对称轴,结合函数的定义域,即可求得总利润y的最大值.
(1)由已知y1=
 ,y2=
,y2=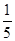 (3-x)
(3-x)∴y=y1+y2=
 +
+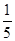 (3-x)
(3-x)自变量x的的取值范围为0≤x≤3;
(2)∵
 =t,∴x=t2,
=t,∴x=t2, ∴y=
 +
+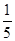 (3-t2)=-
(3-t2)=-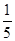 t2+
t2+ +
+ =-
=-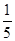 ( t-
( t-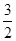 )2+
)2+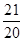
∴当t=
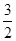 时,y取最大值.
时,y取最大值. 由t=
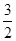 得,x=
得,x=
∴3-x=

即经营甲、乙两种商品分别投入
 、
、 万元时,使得总利润最大.
万元时,使得总利润最大.点评:二次函数的应用是初中数学的重点和难点,在中考中极为常见,一般压轴题形式出现,难度较大.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.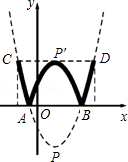
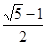 .请你计算这个“W”图案的高与宽的比到底是多少?
.请你计算这个“W”图案的高与宽的比到底是多少? 上.
上.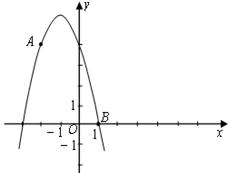
 、n;
、n;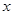 轴上找点D,使得以点B′、C、D为顶点的三角形与
轴上找点D,使得以点B′、C、D为顶点的三角形与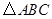 相似.
相似.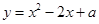 (
(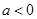 )与
)与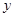 轴相交于点
轴相交于点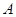 ,顶点为
,顶点为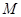 .直线
.直线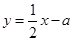 分别与
分别与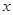 轴,
轴,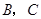 两点,并且与直线
两点,并且与直线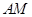 相交于点
相交于点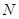 .
.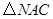 沿
沿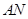 ′与
′与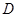 ,连结
,连结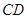 ,求
,求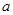 的值和四边形
的值和四边形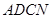 的面积;
的面积;
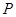 ,使得以
,使得以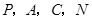 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出
 ,则王刚掷铅球的成绩为 m.
,则王刚掷铅球的成绩为 m. x2﹣7x+
x2﹣7x+ ,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )
,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )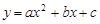 的图象如图所示,那么关于
的图象如图所示,那么关于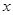 的方程
的方程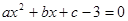 的根的情况是( )
的根的情况是( )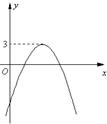
 的自变量
的自变量 与函数
与函数 的对应值,可判断该二次函数的图像与
的对应值,可判断该二次函数的图像与