题目内容
已知抛物线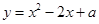 (
(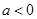 )与
)与 轴相交于点
轴相交于点 ,顶点为
,顶点为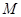 .直线
.直线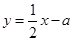 分别与
分别与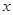 轴,
轴,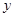 轴相交于
轴相交于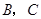 两点,并且与直线
两点,并且与直线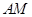 相交于点
相交于点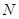 .
.
(1)如图,将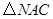 沿
沿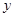 轴翻折,若点
轴翻折,若点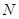 的对应点
的对应点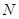 ′恰好落在抛物线上,
′恰好落在抛物线上,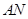 ′与
′与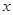 轴交于点
轴交于点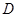 ,连结
,连结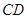 ,求
,求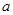 的值和四边形
的值和四边形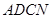 的面积;
的面积;
(2)在抛物线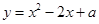 (
(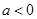 )上是否存在一点
)上是否存在一点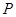 ,使得以
,使得以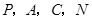 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出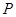 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
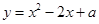 (
(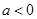 )与
)与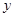 轴相交于点
轴相交于点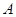 ,顶点为
,顶点为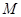 .直线
.直线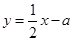 分别与
分别与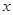 轴,
轴,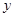 轴相交于
轴相交于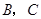 两点,并且与直线
两点,并且与直线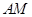 相交于点
相交于点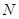 .
.(1)如图,将
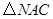 沿
沿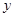 轴翻折,若点
轴翻折,若点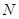 的对应点
的对应点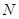 ′恰好落在抛物线上,
′恰好落在抛物线上,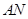 ′与
′与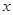 轴交于点
轴交于点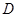 ,连结
,连结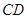 ,求
,求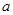 的值和四边形
的值和四边形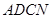 的面积;
的面积;
(2)在抛物线
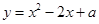 (
(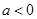 )上是否存在一点
)上是否存在一点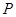 ,使得以
,使得以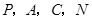 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出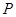 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.(1)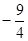 ,
,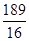 ;(2)
;(2)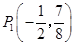 或
或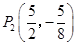
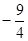 ,
,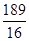 ;(2)
;(2)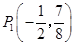 或
或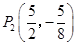
试题分析:(1)先求得
 ,由题意得点
,由题意得点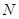 与点
与点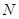 ′关于
′关于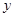 轴对称,即可得到点
轴对称,即可得到点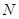 ′的坐标,从而求得a的值,即得点
′的坐标,从而求得a的值,即得点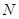 到
到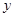 轴的距离为3,再根据待定系数法求得直线
轴的距离为3,再根据待定系数法求得直线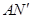 的解析式,再求得它与
的解析式,再求得它与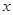 轴的交点坐标,即可得到四边形
轴的交点坐标,即可得到四边形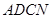 的面积;
的面积;(2)当点
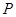 在
在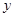 轴的左侧时,若
轴的左侧时,若 是平行四边形,则
是平行四边形,则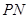 平行且等于
平行且等于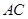 ,则把
,则把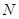 向上平移
向上平移 个单位得到
个单位得到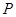 ,坐标为
,坐标为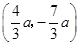 ,代入抛物线的解析式即可求得点P的坐标;当点
,代入抛物线的解析式即可求得点P的坐标;当点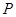 在
在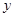 轴的右侧时,若
轴的右侧时,若 是平行四边形,则
是平行四边形,则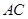 与
与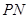 互相平分,即可得到点P的坐标.
互相平分,即可得到点P的坐标.(1)

由题意得点
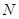 与点
与点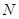 ′关于
′关于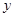 轴对称,
轴对称,
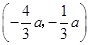 ,
,将
 ′的坐标代入
′的坐标代入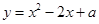 得
得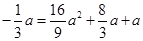 ,
,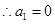 (舍去),
(舍去),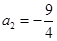
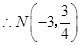 ,
, 点
点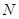 到
到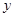 轴的距离为3.
轴的距离为3.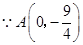 ,
,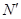
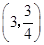 ,
, 直线
直线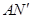 的解析式为
的解析式为 ,
,它与
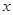 轴的交点为
轴的交点为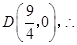 点
点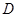 到
到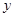 轴的距离为
轴的距离为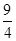 .
.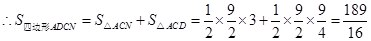
(2)当点
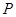 在
在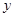 轴的左侧时,若
轴的左侧时,若 是平行四边形,则
是平行四边形,则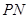 平行且等于
平行且等于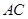 ,
, 把
把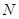 向上平移
向上平移 个单位得到
个单位得到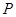 ,坐标为
,坐标为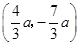 ,代入抛物线的解析式,
,代入抛物线的解析式,得:

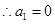 (不舍题意,舍去),
(不舍题意,舍去),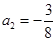 ,
,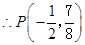
当点
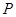 在
在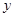 轴的右侧时,若
轴的右侧时,若 是平行四边形,则
是平行四边形,则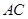 与
与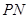 互相平分,
互相平分, .
. 与
与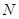 关于原点对称,
关于原点对称,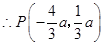 ,
,将
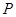 点坐标代入抛物线解析式得:
点坐标代入抛物线解析式得: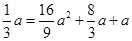 ,
,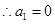 (不合题意,舍去),
(不合题意,舍去), ,
,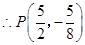 .
. 存在这样的点
存在这样的点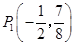 或
或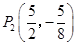 ,能使得以
,能使得以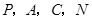 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在直线AQ上.设点P的运动时间为t(s).
cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在直线AQ上.设点P的运动时间为t(s).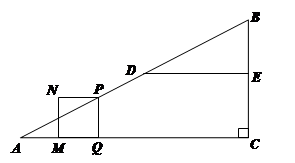
 过点A(0,4)和C(8,0),P(t,0)是
过点A(0,4)和C(8,0),P(t,0)是 轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过B作
轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过B作 轴的垂线,两直线相交于点D.
轴的垂线,两直线相交于点D.

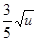 ,y2=
,y2=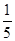 u.如果将3万元资金投入经营甲、乙两种商品,其中对甲商品的投资为x(万元).
u.如果将3万元资金投入经营甲、乙两种商品,其中对甲商品的投资为x(万元). =t,试写出y关于t的函数关系式,并求出经营甲、乙两种商品各投入多少万元时使得总利润最大.
=t,试写出y关于t的函数关系式,并求出经营甲、乙两种商品各投入多少万元时使得总利润最大. 的顶点坐标是
的顶点坐标是 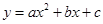 的自变量
的自变量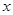 与函数值
与函数值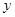 的对应值,判断方程
的对应值,判断方程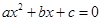 (
(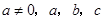 为常数)的一个解
为常数)的一个解
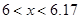 B
B 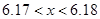 C.
C.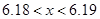 D.
D.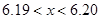
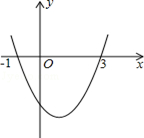
 ,下面四条信息:
,下面四条信息: