Question

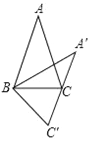
【题目】如图，在△ABC中，AB=AC，将△ABC绕顶点B顺时针旋转，得到△A′BC′．设∠A=α，当A′C′恰好经过顶点C时，∠A′BC=_____（用含α的式子表示）．

Answer 1

【答案】90°﹣

【解析】根据等腰三角形的性质和三角形的内角和得到∠ABC=∠ACB=90°﹣，由旋转的性质有∠A′BC′=∠ABC=∠A′BC=∠C′=90°﹣，CB=C′B，根据等腰三角形的性质得到∠BCC′=90°﹣，于是得到结论．

解：∵AB=AC，∠A=α，

∴∠ABC=∠ACB=90°﹣，

由旋转的性质有∠A′BC′=∠ABC=∠A′BC=∠C′=90°﹣，CB=C′B，

∴∠BCC′=90°﹣，

∴∠CBC′=∠A=α，

∴∠A′BC=∠A′BC′﹣∠CBC′=90°﹣﹣α=90°﹣．

故答案为：90°﹣．

“点睛”本题考查了旋转的性质等腰三角形的性质，三角形的内角和，熟练掌握旋转的性质是解题的关键．