题目内容
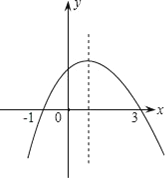
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】试题分析:①由二次函数y=ax2+bx+c(a≠0)的开口向下,可知a<0,故错误;
②由二次函数与x轴的交点的坐标为(-1,0),(3,0),可知对称轴为x=![]() =1,即-
=1,即-![]() =1,
=1,
因此可得b=-2a,即2a+b=0,故正确;
③由函数的顶点在第一象限,因此可知,当x=1时,y=a+b+c>0,故正确;
④由二次函数与x轴的交点的坐标为(-1,0),(3,0),图象开口向下,因此当-1<x<3时,y>0,故正确.
共3个正确的.
故选C

练习册系列答案
相关题目
【题目】某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q = W + 100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
次数n | 2 | 1 |
速度x | 40 | 60 |
指数Q | 420 | 100 |
(1)用含x和n的式子表示Q;
(2)当x = 70,Q = 450时,求n的值;
(3)若n = 3,要使Q最大,确定x的值;
(4)设n = 2,x = 40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420,若能,求出m的值;若不能,请说明理由.