题目内容
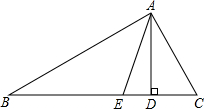
如图，△ABC中，角平分线AD、BE、CF相交于点H，过H点作HG⊥AC，垂足为G，那么∠AHE和∠CHG的大小关系为（ ）
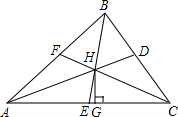
| A．∠AHE＞∠CHG | B．∠AHE＜∠CHG | C．∠AHE=∠CHG | D．不一定 |
∵AD、BE、CF为△ABC的角平分线
∴可设∠BAD=∠CAD=x，∠ABE=∠CBE=y，∠BCF=∠ACF=z，
∴2x+2y+2z=180°即x+y+z=90°
∵在△AHB中，∠AHE=x+y=90°-z，
在△CHG中，∠CHG=90°-z，
∴∠AHE=∠CHG．
故选C．
∴可设∠BAD=∠CAD=x，∠ABE=∠CBE=y，∠BCF=∠ACF=z，
∴2x+2y+2z=180°即x+y+z=90°
∵在△AHB中，∠AHE=x+y=90°-z，
在△CHG中，∠CHG=90°-z，
∴∠AHE=∠CHG．
故选C．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
