题目内容
【题目】再读教材:
宽与长的比是 
(约为0.618)的矩形叫做黄金矩形，黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计，下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步，如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
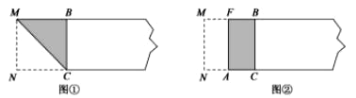
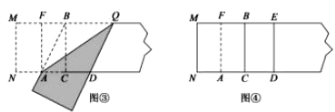
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处，
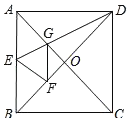
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形，
问题解决:
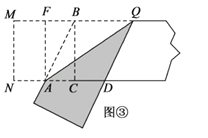
（1）图③中AB=________(保留根号);
（2）如图③,判断四边形 BADQ的形状,并说明理由;
（3）请写出图④中所有的黄金矩形,并选择其中一个说明理由.
（4）结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
【答案】（1）
；(2)见解析;(3) 见解析; (4) 见解析.
【解析】（1）由勾股定理计算即可；
（2）根据菱形的判定方法即可判断；
（3）根据黄金矩形的定义即可判断；
（4）如图④﹣1中，在矩形BCDE上添加线段GH，使得四边形GCDH为正方形，此时四边形BGHE为所求是黄金矩形．
（1）如图3中．在Rt△ABC中，AB=
=
=．
故答案为：．
（2）结论：四边形BADQ是菱形．理由如下：
如图③中，∵四边形ACBF是矩形，∴BQ∥AD．
∵AB∥DQ，∴四边形ABQD是平行四边形，由翻折可知：AB=AD，∴四边形ABQD是菱形．
（3）如图④中，黄金矩形有矩形BCDE，矩形MNDE．
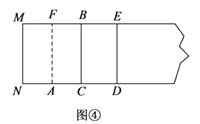
∵AD=．AN=AC=1，CD=AD﹣AC=﹣1．
∵BC=2，∴
=
，∴矩形BCDE是黄金矩形．
∵
=
=，∴矩形MNDE是黄金矩形．
（4）如图④﹣1中，在矩形BCDE上添加线段GH，使得四边形GCDH为正方形，此时四边形BGHE为所求是黄金矩形．
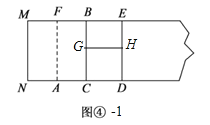
长GH=﹣1，宽HE=3﹣．
