题目内容
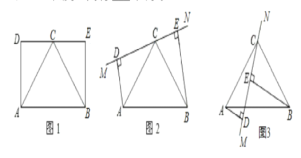
【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
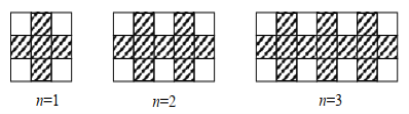
(1)铺第5个图形用黑色正方形瓷砖 块;
(2)按照此方式铺下去,铺第 n 个图形用黑色正方形瓷砖 块;(用含 n的代数式表示)
(3)若黑、白两种颜色的瓷砖规格都为( 长0.5米宽0.5米),且黑色正方形瓷砖每块价格 25 元,白色正方形瓷砖每块价格30元,若按照此方式恰好铺满该小路某一段(该段小路的总面积为 18.75 平方米),求该段小路所需瓷砖的总费用.
【答案】(1)21;(2)4n+1;(3)2005元.
【解析】
(1)根据题意构造出第五个图形的形状,数黑色正方形瓷砖的块数,即可得出答案;
(2)多画几个图形,总结规律,即可得出答案;
(3)分别求出黑白两种瓷砖的块数,乘以各自的价格即可得出答案.
解:(1)由题意可得,铺第5个图形用黑色正方形瓷砖21块;
(2)铺第1个图形用黑色正方形瓷砖5块
铺第2个图形用黑色正方形瓷砖9=5+4块
铺第3个图形用黑色正方形瓷砖13=5+4+4块
铺第4个图形用黑色正方形瓷砖17=5+4+4+4块
铺第5个图形用黑色正方形瓷砖21=5+4+4+4+4块
……
∴铺第n个图形用黑色正方形瓷砖5+4(n-1)=4n+1块
故答案为:4n+1.
(3)18.75÷(0.5×0.5)=75(块)
由题意可得,铺第n个图形共用正方形瓷砖9+6(n-1)=6n+3块,铺第n个图形用白色正方形瓷砖4+2(n-1)=2n+2块
6n+3=75,解得:n=12
可知,第12个图形用黑色正方形:4×12+1=49块,用白色正方形:2×12+2=26块
所以总费用=49×25+26×30=2005(元)
答:该段小路所需瓷砖的总费用为2005元.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】七年级一班和二班各推选![]() 名同学进行投篮比赛,按照比赛规则,每人各投了
名同学进行投篮比赛,按照比赛规则,每人各投了![]() 个球,两个班选手的进球数统计如下表,请根据表中数据回答问题.
个球,两个班选手的进球数统计如下表,请根据表中数据回答问题.
进球数(个) |
|
|
|
|
|
|
一班人数(人) |
|
|
|
|
|
|
二班人数(人) |
|
|
|
|
|
|
![]() 填表;
填表;
平均数 | 中位数 | 众数 | 方差 | |
一班 | 2.6 | |||
二班 | 7 | 7 | 7 |
![]() 如果要从这两个班中选出一个班代表级部参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
如果要从这两个班中选出一个班代表级部参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?