题目内容
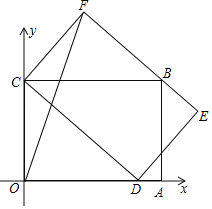
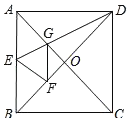
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DF分别交AB、AC于点E、G,连解FG,下列结论:(1)∠AGD=112.5°;(2)E为AB中点;(3)S△AGD=S△OCD;(4)正边形AEFG是菱形;(5)BE=2OG,其中正确结论的个是( )
A.2B.3C.4D.5
【答案】B
【解析】
利用翻折不变性可知:AG=GF,AE=EF,∠ADG=∠GDF=22.5°,再通过角度计算证明AE=AG,即可得到答案,具体见详解.
因为∠GAD=∠ADO=45°,由折叠可知:∠ADG=∠ODG=22.5°.
(1)∠AGD=180°﹣45°﹣22.5°=112.5°,故(1)正确;
(2)设OG=1,则AG=GF=![]() ,
,
又∠BAG=45°,∠AGE=67.5°,∴∠AEG=67.5°,
∴AE=AG=![]() ,则AC=2AO=2(
,则AC=2AO=2(![]() +1),
+1),
∴AB=![]() =2+
=2+![]() ,
,
∴AE≠EB,故(2)错误;
(3)由折叠可知:AG=FG,在直角三角形GOF中,
斜边GF>直角边OG,故AG>OG,两三角形的高相同,
则S△AGD>S△OGD,故(3)错误;
(4)中,AE=EF=FG=AG,故(4)正确;
(5)∵GF=EF,
∴BE=![]() EF=
EF=![]() GF=
GF=![]()
![]() OG=2OG,
OG=2OG,
∴BE=2OG,故(5)正确.
故选:B.

练习册系列答案
相关题目