题目内容
【题目】阅读下面材料．
在数学课上，老师请同学思考如下问题：
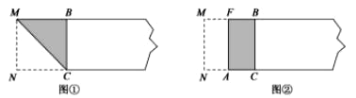
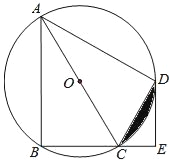
已知：如图①，在△ABC中，∠A＝90°.
图①
求作：⊙P，使得点P在边AC上，且⊙P与AB，BC都相切．
小轩的主要作法如下：
如图②，
图②
(1)作∠ABC的平分线BF，与AC交于点P；
(2)以P为圆心，AP长为半径作⊙P，则⊙P即为所求．
老师说：“小轩的作法正确．”
请回答：⊙P与BC相切的依据是 ____．
【答案】角平分线上的点到角两边的距离相等；若圆心到直线的距离等于半径，则这条直线为圆的切线
【解析】作PD⊥BC，根据角平分线上的点到角两边的距离相等，易得PD=PA，根据切线的判定定理可证得BC是⊙P的切线.
如答图，过点P作PD⊥BC于点D，
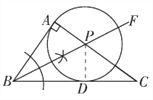
∵BF平分∠ABC，∠A＝90°，
∴PA＝PD，
∴⊙P与BC相切．
练习册系列答案
相关题目
