[题目]已知.K是图中所示正方体中棱CD的中点.连接KE.AE.则cos∠KEA的值为．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知，K是图中所示正方体中棱CD的中点，连接KE、AE，则cos∠KEA的值为．

【答案】
【解析】连接AK．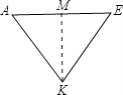

设正方体的棱长为a．由勾股定理，得AE= a，AK=EK= a．

过点K作KM⊥AE于M，则AM=EM= AE= a．

在直角三角形KEM中，∠KME=90°，∴cos∠KEA= = = = ．

【考点精析】认真审题，首先需要了解等腰三角形的性质(等腰三角形的两个底角相等（简称：等边对等角）)，还要掌握正方形的性质(正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键．

练习册系列答案

相关题目

【题目】正方形ABCD、正方形BEFG和正方形DMNK的位置如图所示，点A在线段NF上，AE=8，则△NFP的面积为（）．

A.30
B.32
C.34
D.36

【题目】下面是由同一型号的黑白两种颜色的等边三角形瓷砖按一定规律铺设的图形.仔细观察图形可知：

第1个图形中有1块黑色的瓷砖，可表示为；

第2个图形中有3块黑色的瓷砖，可表示为；

第3个图形中有6块黑色的瓷砖，可表示为；

则第个图形中有__________块黑色的瓷砖（为正整数）．

【题目】已知数轴上三点、、表示的数分别为4、0、，动点从点出发，以每秒3个单位的速度沿数轴向左匀速运动.

（1）当点到点的距离与点到点的距离相等时，点在数轴上表示的数是 .

（2）另一动点从点出发，以每秒2个单位的速度沿数轴向左匀速运动，若点、同时出发，问点运动多长时间追上点？

（3）若点为的中点，点为的中点，点在运动过程中，线段的长度是否发生变化？若发生变化，请你说明理由；若不变，请你画出图形，并求出线段的长度.

【题目】阅读理解：

类比定义：我们知道：分式和分数有着很多的相似点.如类比分数的基本性质，我们得到了分式的基本性质；类比分数的运算法则，我们得到了分式的运算法则等等.小学里，把分子比分母小的分数叫做真分数，类似地，我们把分子整式的次数小于分母整式的次数的分式称为真分式；反之，称为假分式.

拓展定义：

对于任何一个分式都可以化成整式与真分式的和的形式，

如：；

理解定义：

（1）下列分式中，属于真分式的是：____属于假分式的是：_____（填序号）

①；②；③；④.

拓展应用：

（2）将分式化成整式与真分式的和的形式；

（3）将假分式化成整式与真分式的和的形式。

【题目】如图，在边长均为1个单位的正方形网格图中，建立了平面直角坐标系xOy，按要求解答下列问题：

（1）写出△ABC三个顶点的坐标；

（2）画出△ABC向右平移6个单位后得到的图形△A1B1C1；

（3）求△ABC的面积．

【题目】解不等式组：请结合题意填空，完成本题的解答：
（i）解不等式（1），得；
（ii）解不等式（2），得；
（iii）把不等式（1）和（2）的解集在数轴上表示出来：

（iv）原不等式的解集为：．

【题目】某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售2辆A型车和1辆B型车，销售额为62万元．

（1）求每辆A型车和B型车的售价各多少万元．

（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元. 则有哪几种购车方案?

【题目】如果两个三角形的两条边对应相等，夹角互补，那么这两个三角形叫做互补三角形，如图2，分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF，则图中的两个三角形就是互补三角形．

（1）用尺规将图1中的△ABC分割成两个互补三角形；
（2）证明图2中的△ABC与△AEF两个互补三角形面积相等；
（3）如图3，在图2的基础上再以BC为边向外作正方形BCHI．
①已知三个正方形面积分别是17、13、10，在如图4的网格中（网格中每个小正方形的边长为1）画出边长为、、的三角形，并计算图3中六边形DEFGHI的面积．
②若△ABC的面积为2，求以EF、DI、HG的长为边的三角形面积．

试题分类