题目内容
【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.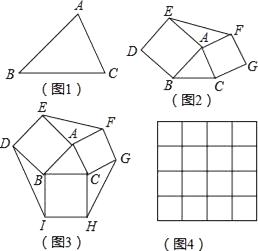
(1)用尺规将图1中的△ABC分割成两个互补三角形;
(2)证明图2中的△ABC与△AEF两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI.
①已知三个正方形面积分别是17、13、10,在如图4的网格中(网格中每个小正方形的边长为1)画出边长为 ![]() 、
、 ![]() 、
、 ![]() 的三角形,并计算图3中六边形DEFGHI的面积.
的三角形,并计算图3中六边形DEFGHI的面积.
②若△ABC的面积为2,求以EF、DI、HG的长为边的三角形面积.
【答案】
(1)解:如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形.
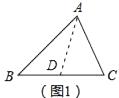
(2)解:如图2中,延长FA到点H,使得AH=AF,连接EH.

∵四边形ABDE,四边形ACGF是正方形,
∴AB=AE,AF=AC,∠BAE=∠CAF=90°,
∴∠EAF+∠BAC=180°,
∴△AEF和△ABC是两个互补三角形.
∵∠EAH+∠HAB=∠BAC+∠HAB=90°,
∴∠EAH=∠BAC,
∵AF=AC,
∴AH=AC,
在△AEH和△ABC中,
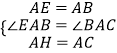
∴△AEH≌△ABC,
∴S△AEF=S△AEH=S△ABC.
(3)解:①边长为 ![]() 、
、 ![]() 、
、 ![]() 的三角形如图4所示.
的三角形如图4所示.

∵S△ABC=3×4﹣2﹣1.5﹣3=5.5,
∴S六边形=17+13+10+4×5.5=62.
②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,

∵AM∥CH,CH⊥BC,
∴AM⊥BC,
∴∠EAM=90°+90°﹣x=180°﹣x,
∵∠DBI=360°﹣90°﹣90°﹣x=180°﹣x,
∴∠EAM=∠DBI,∵AE=BD,
∴△AEM≌△DBI,
∵在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,
∴△DBI和△ABC是互补三角形,
∴S△AEM=S△AEF=S△AFM=2,
∴S△EFM=3S△ABC=6.
【解析】(1)作BC边上的中线AD,根据三角形中线的定义知BD=CD,AD=AD,根据领补角的定义![]() +
+![]() =180
=180![]() ,根据互补三角形的定义△ABD和△ADC是互补三角形;
,根据互补三角形的定义△ABD和△ADC是互补三角形;
(2)延长FA到点H,使得AH=AF,连接EH.根据正方形的性质AB=AE,AF=AC,∠BAE=∠CAF=90°,根据周角的定义知∠EAF+∠BAC=180°,根据互补三角形的定义得出△AEF和△ABC是两个互补三角形,根据同角的余角相等得出∠EAH=∠BAC,根据正方形的性质及作的辅助线知AH=AC,进而利用SAS判断出△AEH≌△ABC,从而根据全等三角形的面积相等得出S△AEH=S△ABC,由根据等底同高的两个三角形面积相等得出S△AEF=S△AEH,从而得出S△AEF=S△AEH=S△ABC;
(3)①利用勾股定理,结合网格结构画出边长为![]() ,
,![]() ,
,![]() 的三角形即可;利用割补法求面积即可;②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,根据平行线的性质得出AM⊥BC,根据垂直的定义得出∠EAM=90°+90°﹣x=180°﹣x,根据周角的定义,及等量代换得出∠EAM=∠DBI,从而判断出△AEM≌△DBI,在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,根据互补三角形的定义知△DBI和△ABC是互补三角形,然后得出结论。
的三角形即可;利用割补法求面积即可;②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,根据平行线的性质得出AM⊥BC,根据垂直的定义得出∠EAM=90°+90°﹣x=180°﹣x,根据周角的定义,及等量代换得出∠EAM=∠DBI,从而判断出△AEM≌△DBI,在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,根据互补三角形的定义知△DBI和△ABC是互补三角形,然后得出结论。
【考点精析】掌握三角形的面积和正方形的性质是解答本题的根本,需要知道三角形的面积=1/2×底×高;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.





