题目内容
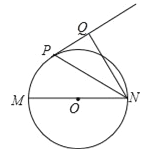
【题目】在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.
(1)求证:BC是⊙O的切线;
(2)若⊙O的直径为10,AE=6,求图中阴影部分的面积.
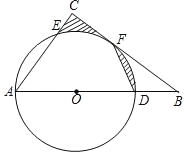
【答案】(1)证明详见解析;(2) 4.
【解析】
试题分析:(1)连接OF,AF,由题意得出![]() ,由圆周角定理和等腰三角形的性质得出∠1=∠3,证出AC∥OF,得出∠BFO=∠ACB=90°,即可得出结论;
,由圆周角定理和等腰三角形的性质得出∠1=∠3,证出AC∥OF,得出∠BFO=∠ACB=90°,即可得出结论;
(2)连接ED,交OF于H,由圆周角定理得出∠AED=90°,由勾股定理求出ED=8,证明四边形ECFH为矩形,得出∠EHO=90°,OF⊥ED,由三角形中位线定理得出OH=![]() =3,求出HF=5﹣3=2,得出
=3,求出HF=5﹣3=2,得出![]() =4,证出阴影部分的面积与△CEF的面积相等,即可得出答案.
=4,证出阴影部分的面积与△CEF的面积相等,即可得出答案.
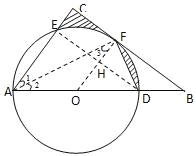
试题解析:(1)连接OF,AF如图,
∵F为![]() 的中点,
的中点,
∴![]() ,
,
∴∠1=∠2,
∵AO=FO,
∴∠3=∠2,
∴∠1=∠3,
∴AC∥OF,
∴∠BFO=∠ACB=90°,
∵F为⊙O上一点,
∴BC为⊙O的切线;
(2)连接ED,交OF于H,如图,
∵AD为⊙O的直径,
∴∠AED=90°,
在Rt△ADE中,ED=![]() =8,
=8,
∵∠AED=90°=∠ACF=∠BFO,
∴四边形ECFH为矩形,
∴∠EHO=90°,OF⊥ED,
∴H为ED的中点,
∴EH=4,
∵O为AD的中点,
∴OH=![]() =3,
=3,
∴HF=5﹣3=2,
∴![]() =4,
=4,
∵![]() ,
,
∴弓形FD与弓形EF全等,
∴阴影部分的面积与△CEF的面积相等,
故图中阴影部分的面积为4.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目