题目内容
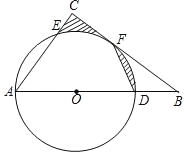
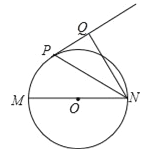
【题目】如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=2,NP=![]() ,求NQ的长.
,求NQ的长.
【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)连结OP,根据切线的性质由直线PQ与⊙O相切得OP⊥PQ,再由OP=ON得到∠ONP=∠OPN,由NP平分∠MNQ得到∠ONP=∠QNP,利用等量代换得∠OPN=∠QNP,根据平行线的判定得OP∥NQ,所以NQ⊥PQ;
(2)连结PM,根据圆周角定理由MN是⊙O的直径得到∠MPN=90°,易证得Rt△NMP∽Rt△NPQ,然后利用相似比可计算出NQ的长.
试题解析:(1)证明:连结OP,如图,∴直线PQ与⊙O相切,∴OP⊥PQ,∵OP=ON,∴∠ONP=∠OPN,∵NP平分∠MNQ,∴∠ONP=∠QNP,∴∠OPN=∠QNP,∴OP∥NQ,∴NQ⊥PQ;
(2)连结PM,如图,∵MN是⊙O的直径,∴∠MPN=90°,∵NQ⊥PQ,∴∠PQN=90°,而∠MNP=∠QNP,∴Rt△NMP∽Rt△NPQ,∴![]() ,即
,即![]() ,∴NQ=3.
,∴NQ=3.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】为了解居民用水情况,在某小区随机抽查了15户家庭的月用水量,结果如下表:
月用水量(吨) | 4 | 5 | 6 | 8 | 9 |
户数 | 2 | 5 | 6 | 1 | 1 |
则这15户家庭的月用水量的众数与中位数分别为( )
A.5、5B.5、6C.6、6D.9、6