题目内容
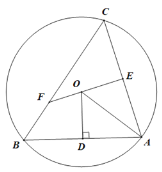
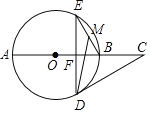
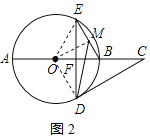
【题目】如图,点C是⊙O的直径AB延长线上一点,过⊙O上一点D作DF⊥AB于F,交⊙O于点E,点M是BE的中点,AB=4,∠E=∠C=30°.
(1)求证:CD是⊙O的切线;
(2)求DM的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,由圆周角定理得出∠DOC=2∠E=60°,∠ODC=180°﹣(∠DOC+∠C)=90°,即可得出结论;
(2)连接OE、OM,证明∠DOC=∠COE=60°,由OB=OE,点M是BE的中点,得出∠BOM=![]() ∠COE=30°,OM⊥BE,则∠DOM=∠DOC+∠BOM=90°,OM=OBcos∠BOM=
∠COE=30°,OM⊥BE,则∠DOM=∠DOC+∠BOM=90°,OM=OBcos∠BOM=![]() ,由勾股定理得DM=
,由勾股定理得DM=![]() =
=![]() .
.
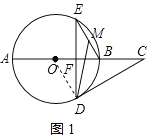
(1)证明:连接OD,如图1所示:
∵∠E=30°,
∴∠DOC=2∠E=60°,
∴∠DOC+∠C=60°+30°=90°,
∴∠ODC=180°﹣(∠DOC+∠C)=180°﹣90°=90°,即OD⊥CD,
∵OD是⊙O的半径,
∴CD是⊙O的切线;
(2)解:连接OE、OM,如图2所示:
∵⊙O的直径AB,AB=4,
∴OB=OD=2,
∵OD=OE,DF⊥AB,
∴∠DOC=∠COE=60°,
∵OB=OE,点M是BE的中点,
∴∠BOM=![]() ∠COE=30°,OM⊥BE,
∠COE=30°,OM⊥BE,
∴∠DOM=∠DOC+∠BOM=60°+30°=90°,
∵在Rt△OMB中,∠OMB=90°,
∴OM=OBcos∠BOM=2cos30°=2×![]() =
=![]() ,
,
由勾股定理得:DM=![]() =
=![]() =
=![]() .
.

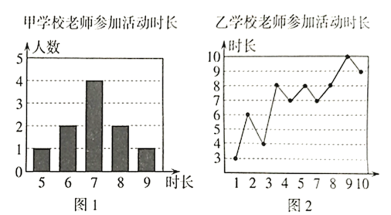
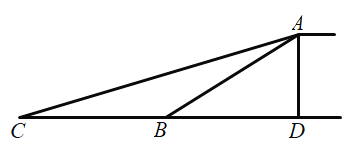
【题目】甲、乙两所学校选派相同人数的老师参加志愿者活动,參加活动时长分别被制成下列两个统计图,根据以上信息,整理分析数据如下表:
平均时间/小时 | 中位数/小时 | 众数/小时 | 方差/小时 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
![]() 求出表格中
求出表格中![]() 的值.
的值.
![]() 分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?
分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?