题目内容
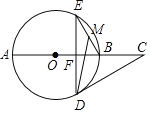
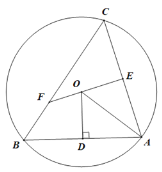
【题目】如图所示,△ABC是圆O的内接三角形,过点O作OD⊥AB与点D,连接OA,点E是AC的中点,延长EO交BC于点F.
(1)求证:△CEF∽△ODA.
(2)若![]() ,△ABC是不是等腰三角形?并说明理由.
,△ABC是不是等腰三角形?并说明理由.
【答案】(1)见解析;(2)是,证明见解析.
【解析】
(1)利用圆周角定理可知∠ECF=![]() ∠AOB,再由垂径定理得到∠AOD=
∠AOB,再由垂径定理得到∠AOD=![]() ∠AOB,从而证明∠ECF=∠AOD,再由垂径定理可得∠ODA=∠CEF=90°,由此即可得出结论;
∠AOB,从而证明∠ECF=∠AOD,再由垂径定理可得∠ODA=∠CEF=90°,由此即可得出结论;
(2)由已知易证△OEC∽△CEF,从而可得∠ECF=∠EOC,再根据圆周角定理证明∠EOC=∠CBA,从而可得∠ECF=∠CBA,由等角对等边即可得出结论.
证明:(1)连接OB,

∵![]() ,
,
∴∠ECF=![]() ∠AOB,
∠AOB,
又∵OD⊥AB,OA=OB,
∴∠AOD=![]() ∠AOB,
∠AOB,
∴∠ECF=∠AOD,
∵OD⊥AB ,
∴∠ODA=90°,
∵E为AC中点 ,
∴OE⊥AC,
∴∠CEF=90°,
∴△CEF∽△ODA.
(2)∵OE·EF=CE2,∠OEC=∠CEF,
∴△OEC∽△CEF,
∴∠ECF=∠EOC,
∵∠EOC=![]() ,∠CBA=
,∠CBA=![]()
∴∠ECF=∠CBA,
∴△ABC是等腰三角形.

练习册系列答案
相关题目