题目内容
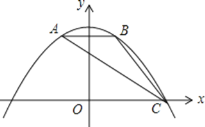
【题目】如图,将三角形纸片![]() 放在平面直角坐标系中,
放在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,点B在x轴的正半轴上,点
,点B在x轴的正半轴上,点![]() 是边
是边![]() 上的一个动点(点P不与点O、B重合),过点P作
上的一个动点(点P不与点O、B重合),过点P作![]() 于点D,沿
于点D,沿![]() 折叠该纸片,使点O落在射线
折叠该纸片,使点O落在射线![]() 上的Q点处.
上的Q点处.
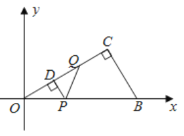
(Ⅰ)用含t的代数式表示线段![]() 的长;
的长;
(Ⅱ)当点Q与点C重合时,求t的值;
(Ⅲ)设![]() 与四边形
与四边形![]() 重叠部分的图形的面积为S,求S与t之间的函数关系式;
重叠部分的图形的面积为S,求S与t之间的函数关系式;
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)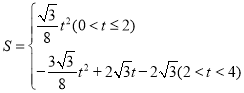 .
.
【解析】
(Ⅰ)解直角三角形求出OC,OD即可解决问题.
(Ⅱ)根据OC=2DC,构建方程求解即可.
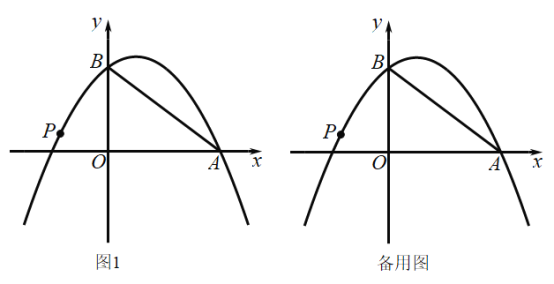
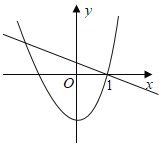
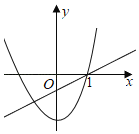
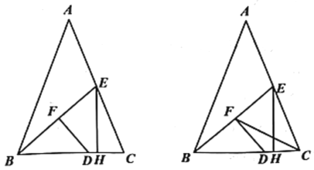
(Ⅲ)分两种情形:如图1中,当0<t≤2时,重叠部分是△PDQ.如图2中,当2<t<4时,重叠部分是四边形PDCH,分别求解即可.
解:(Ⅰ)在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
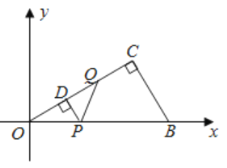
图1
(Ⅱ)∵![]() 于点D,点Q与点C重合,
于点D,点Q与点C重合,
∴![]() ,∴
,∴![]() 垂直平分
垂直平分![]() ,
,
∴![]()
即![]()
∴![]() ;
;
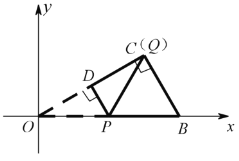
(Ⅲ)当![]() 时,
时,
由(I)得![]() ,
,![]() ,
,
![]() ;
;
当![]() 时,设
时,设![]() 与
与![]() 交于点E
交于点E
![]() ,
,
在![]() 中,
中,![]() ,
,
∴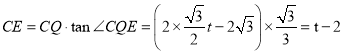 ,
,
∴![]()
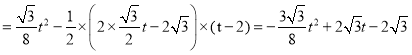
∴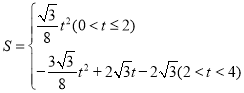 .
.
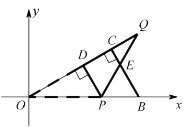
图2

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目