Question

【题目】已知，为的直径，弦于点，在的延长线上取一点，与相切于点，连接交于点.

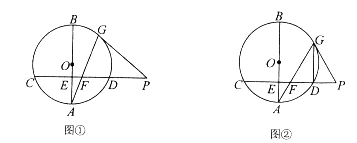
（1）如图①，若，求和的大小；

（2）如图②，若为半径的中点，，且，求的长.

Answer 1

【答案】（1），；（2）.

【解析】

（1）连接，根据直角三角形的两个锐角互余，求得，从而求得的度数，再根据等边对等角和切线的性质求出；

（2）连接，根据和证出，再根据的圆周角所对的弦是直径得出CG为直径，再根据为半径的中点，利用三角函数确定，从而求出GP的长，再根据等角的余角相等证出，从而得出即可.

解：（1）连接，

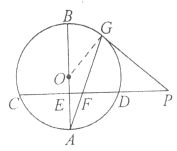
∵于点，

∴.

∵，

∴.

∴.

∵，

∴.

∵与相切于点，

∴.

∴.

（2）连接，

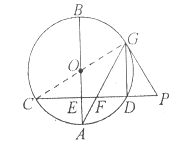
∵于点，

∴.

∵，

∴.

∴为的直径.

∵为半径的中点，

∴.

在中，.

∴.

∵与相切于点，为的直径，

∴.

在中，，

∴.

∵，

∴.

∵，

∴.

∵，

∴.

∴.

∵，

∴.

∴.