题目内容
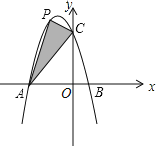
【题目】如图，把
置于平面直角坐标系中，点A的坐标为
，点B的坐标为
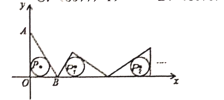
，点P是内切圆的圆心，将沿x轴的正方向作无滑动滚动，使它的三边依次与x轴重合。第一次滚动后，圆心为
，第二次滚动后圆心为
…依次规律，第2019次滚动后，内切圆的圆心
的坐标是（ ）
A.
B.
C.
D.
【答案】C
【解析】
由勾股定理求出AB的长度，从而得出
内切圆的半径，进一步得到点P的坐标，继续由题意得出P3的坐标，找到规律，得出结论即可.
∵点A的坐标为
，点B的坐标为
∴内切圆的半径为
∴点P的坐标为（1,1）
沿y轴的正方向作无滑动滚动，使它的三边依次与x轴重合。第一次滚动后，圆心为
，第二次滚动后圆心为
…
即
每滚动3次一个循环
∵
∴2019次滚动后，内切圆的圆心
的横坐标是
的坐标是
故选C
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
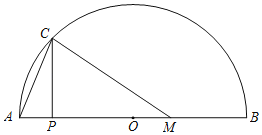
【题目】如图，在半圆弧AB中，直径AB＝6cm，点M是AB上一点，MB＝2cm，P为AB上一动点，PC⊥AB交AB于点C，连接AC和CM，设A、P两点间的距离为xcm，A、C两点间的距离为y1cm，C、M两点间的距离为y2cm．
小东根据学习函数的经验，分别对函数y1、y2随自变量x的变化而变化的规律进行了探究：
下面是小东的探究过程，请补充完整：
（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值；
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.45 | 3.46 | 4.90 | 5.48 | 6 | |
y2/cm | 4 | 3.74 | 3.46 | 3.16 | 2.83 | 2.45 | 2 |
（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出函数y1，y2的图象；
（3）结合函数图象，解决问题：
①当AC＞CM时，线段AP的取值范围是 ；
②当△AMC是等腰三角形时，线段AP的长约为 ．
