题目内容
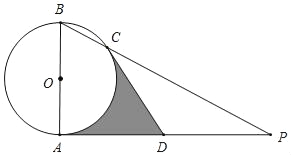
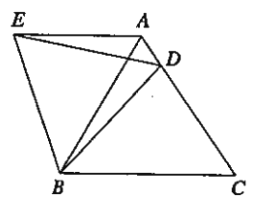
【题目】在等边 ![]() 中,
中,![]() 是边
是边 ![]() 上一点,连接
上一点,连接 ![]() ,将
,将 ![]() 绕点
绕点 ![]() 逆时针旋转
逆时针旋转 ![]() ,得到
,得到 ![]() ,连接
,连接 ![]() ,若
,若 ![]() ,
,![]() ,有下列结论:①
,有下列结论:① ![]() ;②
;② ![]() ;③
;③ ![]() 是等边三角形;④
是等边三角形;④ ![]() 的周长是
的周长是 ![]() .其中,正确结论的个数是
.其中,正确结论的个数是 ![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根据等边三角形的性质得∠ABC=∠C=60°,AC=BC=5,再利用旋转的性质得∠BAE=∠C=60°,AE=CD,则∠BAE=∠ABC,于是根据平行线的判定可对①进行判断;由△BCD绕点B逆时针旋转60°,得到△BAE得到∠DBE=60°,BD=BE=4,则根据边三角形的判定方法得到△BDE为等边三角形,于是可对③进行判断;根据等边三角形的性质得∠BDE=60°,DE=DB=4,然后说明∠BDC>60°,则∠ADE<60°,于是可对②进行判断;最后利用AE=CD,DE=BD=4和三角形周长定义可对④进行判断.
∵△ABC为等边三角形,
∴∠ABC=∠C=60°,AC=BC=5,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠BAE=∠C=60°,AE=CD,
∴∠BAE=∠ABC,
∴AE∥BC,所以①正确;
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠DBE=60°,BD=BE=4,
∴△BDE为等边三角形,所以③正确,
∴∠BDE=60°,DE=DB=4,
在△BDC中,∵BC>BD,
∴∠BDC>∠C,即∠BDC>60°,
∴∠ADE<60°,所以②错误;
∵AE=CD,DE=BD=4,
∴△ADE的周长=AD+AE+DE=AD+CD+DB=AC+BD=5+4=9,所以④正确.
故选:C.

【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.