��Ŀ����
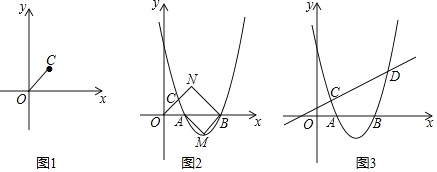
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����C��1��1����������y��ax2+bx+c��a��0������ΪM����x�������ύ��A��B���㣮
��1����ͼ1������OC�����߶�OC�Ƶ�O��ʱ����תʹ��C����y����������ϣ����߶�OC���������
��2����ͼ2���ӳ��߶�OC��N��ʹ��ON��![]() OC������ONA����OBN��tan��BAM��
OC������ONA����OBN��tan��BAM��![]() ���������ߵĽ���ʽ��
���������ߵĽ���ʽ��
��3����ͼ3����֪��ֱ��x��![]() Ϊ�Գ����������y��ax2+bx+c��y���ڣ�0��5������ֱ��l��y��kx+m��k��0����C��D���㣬����x�������ҽ���һ��P��ʹ��CPD��90�㣬��k��ֵ��
Ϊ�Գ����������y��ax2+bx+c��y���ڣ�0��5������ֱ��l��y��kx+m��k��0����C��D���㣬����x�������ҽ���һ��P��ʹ��CPD��90�㣬��k��ֵ��
���𰸡���1��![]() ����2��y��2x2��9x+8����3��k��
����2��y��2x2��9x+8����3��k��![]() ��
��
��������
��1���߶�OC���������![]() ��������
��������![]() ��2��
��2��![]() ��
��
��2����ONA�ס�OBN����OAOB��ON2��4����mn��4���٣��������ߵı���ʽΪ��y��a��x��m����x��n����MH��|yM|����a��![]() ��m����
��m����![]() ��n����
��n����![]() ��AH�T
��AH�T![]() ��m��tan��BAM��
��m��tan��BAM��![]() ��
��![]() a��n��m����
a��n��m����![]() ������ã�a��n��m����
������ã�a��n��m����![]() ���ڣ�����1��1������y��a��x��m����x��n��������ã�a��5��m��n����1���ۣ������٢ڢۼ�����⣻
���ڣ�����1��1������y��a��x��m����x��n��������ã�a��5��m��n����1���ۣ������٢ڢۼ�����⣻
��3�������ߵı���ʽΪ��y��x2��5x+5�����D��m��n����n��m2��5m+5������C��1��1������k��![]() ��m��4������x�������ҽ���һ��P��ʹ��CPD��90�㣬���CD�е��ԲR��x�����У�������⣮
��m��4������x�������ҽ���һ��P��ʹ��CPD��90�㣬���CD�е��ԲR��x�����У�������⣮
��1���߶�OC���������![]() ��������
��������![]() ��2��
��2��![]() ��
��
��2��ON��![]() OC��4�����A��B������ֱ�Ϊ����m��0������n��0����
OC��4�����A��B������ֱ�Ϊ����m��0������n��0����
��ONA����OBN�����ONA�ס�OBN����OAOB��ON2��4����mn��4������
�������ߵı���ʽΪ��y��a��x��m����x��n����
����M��MH��AB��AB�ڵ�H�������ĶԳ���Ϊ��x��![]() ��m+n����
��m+n����
��MH��|yM|����a��![]() ��m����
��m����![]() ��n����
��n����![]() ��
��
AH��xM��xA��![]() ��m
��m
tan��BAM��![]() ��
��![]() a��n��m����
a��n��m����![]() ��
��
����ã�a��n��m����![]() ������
������
����1��1������y��a��x��m����x��n��������ã�a��5��m��n����1������
�����٢ڢ�����ã�m��![]() ��n��
��n��![]() ��a��2��
��a��2��
�������ߵı���ʽΪy��a��x��m����x��n����a��x2��mx��nx+mn����2x2��9x+8��
��3��������ã�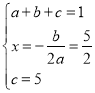 ����ã�
����ã�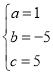 ��
��
�������ߵı���ʽΪ��y��x2��5x+5��
���D��m��n����n��m2��5m+5������C��1��1����
��k��![]() ��m��4��
��m��4��
����x�������ҽ���һ��P��ʹ��CPD��90�㣬���CD�е��ԲR��x�����У����е�ΪP��
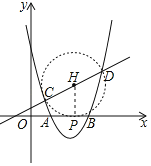
���H��![]() ��
��![]() ������HP��HC��
������HP��HC��
����![]() ��1��2+��
��1��2+��![]() ��1��2����
��1��2����![]() ��2��
��2��
����ã�3m2��18m+19��0��
��ã�m��3+![]() �����������ֵ����ȥ����
�����������ֵ����ȥ����
k��m��4��![]() ��
��

 �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�����Ŀ��Ϊ�˸��ο��ṩ���õķ���ij��������Բ����οͽ����˹��ڡ���������������ȡ��ĵ��飬�����ݵ��������Ƴ����²�������ͳ��ͼ��.
����� | ���� | ��ռ�ٷֱ� |
�dz����� | 12 | 10% |
���� | 54 | m |
�Ƚ����� | n | 40% |
������ | 6 | 5% |

����ͼ����Ϣ������������⣺
(1)���ε����������Ϊ______������m��ֵΪ_______��
(2)�벹ȫ����ͳ��ͼ��
(3)��ͳ�ƣ��þ���ƽ��ÿ��Ӵ��ο�Լ3600�ˣ��������dz����⡱�͡����⡱��Ϊ�οͶԾ����������Ŀ϶���������Ƹþ���������ƽ��ÿ��õ��������ο͵Ŀ϶�.
����Ŀ��Ϊ�˽�Լ��ˮ��ijˮ���涨��ij��Ԫ�������һ���µ���ˮ��������![]() �֣���ô����¸õ�Ԫ����ֻ��10Ԫˮ�ѣ��������
�֣���ô����¸õ�Ԫ����ֻ��10Ԫˮ�ѣ��������![]() �֣�������³�����Ҫ��10Ԫˮ���⣬�����Dz��ְ�ÿ��
�֣�������³�����Ҫ��10Ԫˮ���⣬�����Dz��ְ�ÿ��![]() Ԫ���ѣ�
Ԫ���ѣ�
��1���õ�Ԫ����8�·���ˮ80�֣����������涨��![]() ������������Ӧ��ˮ�� ��80-x��
������������Ӧ��ˮ�� ��80-x��
Ԫ���ú�x��ʽ�ӱ�ʾ����
��2���±��Ǹõ�Ԫ����9�¡�10�µ���ˮ����ͽ��������
�·� | ��ˮ�����֣� | ����������Ԫ�� |
9�·� | 85 | 25 |
10�·� | 50 | 10 |
�����ϱ����ݣ����x���Ƕ��٣�