Question

【题目】（本题满分12分）在平面直角坐标系中，抛物线经过A（－3,0）、B（4,0）两点，且与y轴交于点C，点D在x轴的负半轴上，且BD＝BC，有一动点P从点A出发，沿线段AB以每秒1个单位长度的速度向点B移动，同时另一个动点Q从点C出发，沿线段CA以某一速度向点A移动.

（1）求该抛物线的解析式；

（2）若经过t秒的移动，线段PQ被CD垂直平分，求此时t的值；

（3）该抛物线的对称轴上是否存在一点M，使MQ＋MA的值最小？若存在，求出点M的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）抛物线的解析式为 .（2）t的值为.（3）在抛物线的对称轴上存在一点M（ ， ），使得MQ＋MA的值最小.

【解析】解：（1）∵抛物线经过A（－3,0），B（4,0）两点，

∴ 解得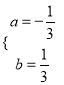

∴所求抛物线的解析式为.

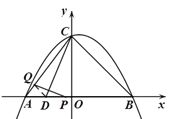
（2）如图，依题意知AP＝t，连接DQ，

由A（－3,0），B（4,0），C（0,4），

可得AC＝5，BC＝ ，AB＝7.

∵BD＝BC，

∴ .

∵CD垂直平分PQ，∴QD＝DP，∠CDQ= ∠CDP.

∵BD＝BC，∴∠DCB= ∠CDB.

∴∠CDQ= ∠DCB.∴DQ∥BC.

∴△ADQ∽△ABC.∴ .∴ .

∴ .解得 .

∴ .

∴线段PQ被CD垂直平分时，t的值为 .

（3）设抛物线的对称轴 与x轴交于点E.

点A、B关于对称轴 对称，连接BQ交该对称轴于点M.

则 ，即.

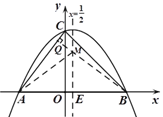
当BQ⊥AC时，BQ最小.

此时，∠EBM= ∠ACO.

∴ .

∴ .∴ ，

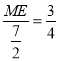解得ME=.

∴M（， ）.

即在抛物线的对称轴上存在一点M（ ， ），使得MQ＋MA的值最小.