题目内容
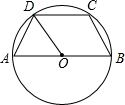
 24、如图,梯形ABCD内接于⊙O,BC∥AD,AC与BD相交于点E,在不添加任何辅助线的情况下:
24、如图,梯形ABCD内接于⊙O,BC∥AD,AC与BD相交于点E,在不添加任何辅助线的情况下:(1)图中共有几对全等三角形,请把它们一一写出来,并选择其中一对全等三角形进行证明;
(2)若BD平分∠ADC,请找出图中与△ABE相似的所有三角形.
分析:(1)已知了BC∥AD,可得出的条件有:弧AB=弧CD,弧AC=弧BD;即AB=CD、AC=BD、∠BAC=∠CDB、∠BCA=∠CBD;再根据AD=AD、∠AEB=∠CED,可得出的全等三角形有:①△ADB≌△DAO(SSS);②△ABE≌△DCE(AAS);③△ABC≌△DCB(AAS).
(2)BD平分∠ADC,那么弧AB=弧BC=弧CD.可根据圆周角定理得出的相等角进行判断.
(2)BD平分∠ADC,那么弧AB=弧BC=弧CD.可根据圆周角定理得出的相等角进行判断.
解答:解:(1)图中共有三对全等三角形:
①△ADB≌△DAC,②△ABE≌△DCE,③△ABC≌△DCB;
选择①△ADB≌△DAC证明:
在⊙O中,∠ABD=∠DCA,∠BCA=∠BDA,
∵BC∥AD,
∴∠BCA=∠CAD.
∴∠CAD=∠BDA.
∵AD=AD,
∴△ADB≌△DAO.
(2)图中与△ABE相似的三角形有:△DCE,△DBA,△ACD.
①△ADB≌△DAC,②△ABE≌△DCE,③△ABC≌△DCB;
选择①△ADB≌△DAC证明:
在⊙O中,∠ABD=∠DCA,∠BCA=∠BDA,
∵BC∥AD,
∴∠BCA=∠CAD.
∴∠CAD=∠BDA.
∵AD=AD,
∴△ADB≌△DAO.
(2)图中与△ABE相似的三角形有:△DCE,△DBA,△ACD.
点评:本题主要考查全等三角形和相似三角形的判定,根据平行线和圆周角定理得出的角和边相等是证三角形全等或相似的关键所在.

练习册系列答案
相关题目
 如图,梯形ABCD内接于⊙O,AB∥CD,AB为直径,DO平分∠ADC,则∠DAO的度数是( )
如图,梯形ABCD内接于⊙O,AB∥CD,AB为直径,DO平分∠ADC,则∠DAO的度数是( )| A、90° | B、80° | C、70° | D、60° |
 如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E,若AD=5,AB=6,BC=9.
如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E,若AD=5,AB=6,BC=9.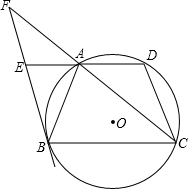 F.
F. 如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为
如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为