题目内容
如图，梯形ABCD内接于⊙O，AD∥BC，E是DA延长线上一点，AB2=AE•BC，BE和CA的延长线交于点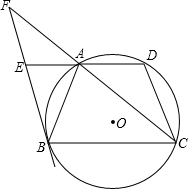
F．（1）求证：BE是⊙O的切线；
（2）已知BC=18，CD=12，AF=16，求BE和AD的长．
分析：（1）连接OA，OB，由三角形相似证明∠1=∠2，再证∠EBO=90，即可证BE是⊙O的切线，
（2）首先由AD∥BC，求出AB、CD，由三角形相似，求出FC，由（1）知△ABC∽△EAB，求出EB，进而求出ED、AB．
（2）首先由AD∥BC，求出AB、CD，由三角形相似，求出FC，由（1）知△ABC∽△EAB，求出EB，进而求出ED、AB．
解答：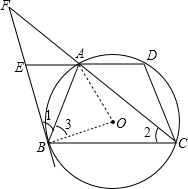
（1）证明：连接OA，OB，
∵AD∥BC，∠ABC=∠EAB，
∵AB2=AE•BE，∴
=
，∴△ABC∽△EAB
∴∠1=∠2（2分）
∵OA=OB，∴∠3=∠BAO，
∴∠O+2∠3=180°
又∵∠O=2∠2，∴2∠2+2∠3=180°，∴∠1+∠3=90°
∴∠EBO=90°，∴OB⊥BF（4分）
又B点在⊙O上，
∴BF是⊙O的切线（5分）
（2）解：∵AD∥BC，AB=CD，
∴AB=CD=12，
∵AB2=AE•BC，∴AE=
=
=8
∵AD∥BC，∴△EFA∽△FBC，∴
=
∴FC=
=36，∴AC=20（7分）
由（1）知△ABC∽△EAB，∴
=
，∴EB=
=
由△EBA∽△EBD（或由切割线定理）得EB2=EA•ED，∴ED=
∴AD=ED-EA=
（9分）
综上，EB=
，AD=
为所求．（10分）
（1）证明：连接OA，OB，∵AD∥BC，∠ABC=∠EAB，
∵AB2=AE•BE，∴
| AB |
| AE |
| BC |
| AB |
∴∠1=∠2（2分）
∵OA=OB，∴∠3=∠BAO，
∴∠O+2∠3=180°
又∵∠O=2∠2，∴2∠2+2∠3=180°，∴∠1+∠3=90°
∴∠EBO=90°，∴OB⊥BF（4分）
又B点在⊙O上，
∴BF是⊙O的切线（5分）
（2）解：∵AD∥BC，AB=CD，
∴AB=CD=12，
∵AB2=AE•BC，∴AE=
| AB2 |
| BC |
| 144 |
| 18 |
∵AD∥BC，∴△EFA∽△FBC，∴
| AE |
| BC |
| FA |
| FC |
∴FC=
| FA×BC |
| AE |
由（1）知△ABC∽△EAB，∴
| EB |
| AC |
| AE |
| AB |
| 20×8 |
| 12 |
| 40 |
| 3 |
由△EBA∽△EBD（或由切割线定理）得EB2=EA•ED，∴ED=
| 200 |
| 9 |
∴AD=ED-EA=
| 128 |
| 9 |
综上，EB=
| 40 |
| 3 |
| 128 |
| 9 |
点评：本题考查了切线的判定，相似三角形等知识点．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．
练习册系列答案
相关题目
24、如图，梯形ABCD内接于⊙O，BC∥AD，AC与BD相交于点E，在不添加任何辅助线的情况下：
如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E，若AD=5，AB=6，BC=9．
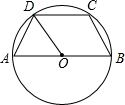如图，梯形ABCD内接于⊙O，AB∥CD，AB为直径，DO平分∠ADC，则∠DAO的度数是（ ）| A、90° | B、80° | C、70° | D、60° |
如图，梯形ABCD内接于⊙O，AD∥BC，∠DAB=49°，则∠AOC的度数为