题目内容
如图，梯形ABCD内接于⊙O，AD∥BC，∠DAB=49°，则∠AOC的度数为分析：如图，在
上取点M，连接AM，CM，根据平行线的性质可以求得：∠ABC=131°，然后根据圆的内接四边形对角互补，即可求得∠ABC的度数，根据圆周角定理求得∠AOC的度数．
 |
| AD |
解答：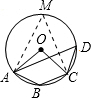
解：如图，在
上取点M，连接AM，CM，
∵AD∥BC，∠DAB=49°，
∴∠ABC=131°，
∴∠M=49°，
∠AOC=98°．
故答案为：98°．
解：如图，在 |
| AD |
∵AD∥BC，∠DAB=49°，
∴∠ABC=131°，
∴∠M=49°，
∠AOC=98°．
故答案为：98°．
点评：本题主要考查圆周角定理、圆的内接四边形的性质、平行线的性质，关键在于作好辅助线，求得∠M的度数．
练习册系列答案
相关题目
24、如图，梯形ABCD内接于⊙O，BC∥AD，AC与BD相交于点E，在不添加任何辅助线的情况下：
如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E，若AD=5，AB=6，BC=9．
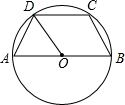如图，梯形ABCD内接于⊙O，AB∥CD，AB为直径，DO平分∠ADC，则∠DAO的度数是（ ）| A、90° | B、80° | C、70° | D、60° |
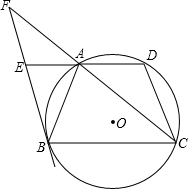F．