题目内容
【题目】如图,⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交⊙O于点D,交BC于点E,连接BD.
(1)线段BD与ID相等吗?证明你的结论.
(2)证明:ID2=DEAD.
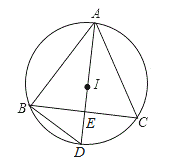
【答案】(1)相等,证明见解析;(2)见解析.
【解析】
(1)连接BI,证∠BIED∠IBD即可;∠IBD=∠4+∠5,∠BID=∠2+∠3;观察上述两个式子:I是△ABC的内心,则∠3=∠4,∠1=∠2;而∠1=∠5,由此可得∠5=∠2;即∠BID=∠IBD,由此得证;(2)由(1)知:ID=BD,即证BE是哪两条线段的比例中项,可通过找以BD为公共边的相似三角形;由(1)证得∠5=∠2,易证得△BED∽△ABD,由此可得出所求的结论.
(1)ID=BD,
理由:∵I是△ABC的内心,
∴∠1=∠2,∠3=∠4;
∵∠BID=∠3+∠2,∠DBI=∠4+∠5,且∠5=∠1,
∴∠BID=∠DBI;
∴ID=BD;
(2)证明:如图所示:
∵∠5=∠1,∠1=∠2;
∴∠5=∠2;
又∵∠D=∠D,
∴△BDE∽△ADB;
∴BD:DE=AD:BD;
∴BD2=ADDE;
又∵ID=BD,
∴ID2=ADDE.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目