题目内容
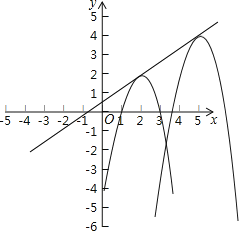
【题目】已知抛物线C1:y=﹣x2+4x﹣3,把抛物线C1先向右平移3个单位长度,再向上平移3个单位长度,得到抛物线C2, 将抛物线C1和抛物线C2这两个图象在x轴及其上方的部分记作图象M.若直线y=kx+ ![]() (k≥0)与图象M至少有2个不同的交点,则k的取值范围是________.
(k≥0)与图象M至少有2个不同的交点,则k的取值范围是________.
【答案】0≤k<10﹣ ![]()
【解析】
首先配方得出二次函数顶点式,求得抛物线C1的顶点坐标,进而利用二次函数平移规律得出抛物线C2,求得直线与两个抛物线相切时的k的值,即可解决问题.
解:
y=-x2+4x-3
=-(x-2)2+1,
∴顶点(2,1)
则将抛物线y=-x2+4x-3先向右平移3个单位长度,再向上平移3个单位长度,
得到的新的抛物线的解析式为:y=-(x-5)2+4=-x2+10x-21.
由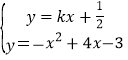 消去y得到x2+(k-4)x+
消去y得到x2+(k-4)x+![]() =0,由题意△=0,(k-4)2-14=0,
=0,由题意△=0,(k-4)2-14=0,
解得k=4-![]() 或4+
或4+![]() (舍弃),
(舍弃),
由 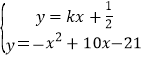 消去y得到x2+(k-10)x+
消去y得到x2+(k-10)x+![]() =0,
=0,
由题意△=0,(k-10)2-86=0,
∴k=10-![]() 或10+
或10+![]() (舍弃),
(舍弃),
∵直线y=kx+![]() (k≥0)与图象M至少有2个不同的交点,
(k≥0)与图象M至少有2个不同的交点,
观察图象可知,则k的取值范围是0≤k<10-![]()

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】某批乒乓球的质量检验结果如下:
抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
优等品频率 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
(1)画出这批乒乓球“优等品”频率的折线统计图;
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于![]() , 问至少取出了多少个黑球?
, 问至少取出了多少个黑球?