题目内容
【题目】有4张正面分别标有数字![]() 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为![]() ,另有一个被均匀分成4份的转盘,上面分别标有数字
,另有一个被均匀分成4份的转盘,上面分别标有数字![]() ,转动转盘,指针所指的数字记为
,转动转盘,指针所指的数字记为![]() (若指针指在分割线上则重新转一次),则点
(若指针指在分割线上则重新转一次),则点![]() 落在抛物线
落在抛物线![]() 与
与![]() 轴所围成的区域内(不含边界)的概率是__________.
轴所围成的区域内(不含边界)的概率是__________.
【答案】![]()
【解析】利用列表法作出所有等可能的情况,然后据二次函数图象上点的坐标特征求出落在抛物线与x轴围成的区域内的点的个数,再根据概率公式列式计算即可得解.
解:列表如下:

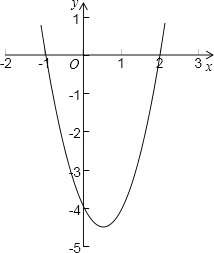
当x=-1时,y=2x2-2x-4=2×(-1)2-2×(-1)-4=2+2-4=0,
所以,没有点落在抛物线与x轴围成的区域内,
当x=0时,y=-4,
所以,没有点落在抛物线与x轴围成的区域内,
当x=![]() 时,y=2x2-2x-4=2×(
时,y=2x2-2x-4=2×(![]() )2-2×
)2-2×![]() -4=
-4=![]() -1-4=-4
-1-4=-4![]() ,
,
所以,点(![]() ,-4)落在抛物线与x轴围成的区域内,当x=-
,-4)落在抛物线与x轴围成的区域内,当x=-![]() 时,y=2x2-2x-4=2×(-
时,y=2x2-2x-4=2×(-![]() )2-2×(-
)2-2×(-![]() )-4=
)-4=![]() +
+![]() -4=-3
-4=-3![]() ,
,
所以,没有点落在抛物线与x轴围成的区域内,
综上所述,点P一共有16种情况,落在抛物线与x轴围成的区域内的点只有(![]() ,-4)一个,
,-4)一个,
所以P(落在抛物线与x轴围成的区域内)=![]() .
.
故答案为:![]() .
.
本题考查了列表法以及概率公式,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
【题目】2019年小张前五个月的奖金变化情况如下表(正数表示比前一月多的钱数,负数表示比前一月少的钱数,单位:元)
月份 | 一月 | 二月 | 三月 | 四月 | 五月 |
钱数变化 |
|
|
|
|
|
若2018年12月份小张的奖金为![]() 元.
元.
(1)用代数式表示2019年二月份小张的奖金为___________元;
(2)小张五月份所得奖金比二月份多多少?