题目内容
【题目】如图,在△ABC中,BC>AC , 点D在BC上,且DC=AC , ∠ACB的平分线CF交AD于F , 点E是AB的中点,连接EF . 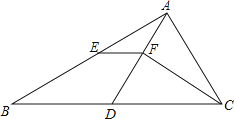
(1)求证:2EF=BD ,
(2)四边形BDFE的面积为6,求△ABD的面积.
【答案】
(1)解答:∵DC=AC,CF为∠ACB的平分线,
∴AF=DF,
∵AE=EB,AF=DF,
∴EF为△ABD的中位线,
∴2EF=BD.
(2)解答:∵EF为△ABD的中位线,
∴EF∥BD,2EF=BD,
∴△AEF∽△ABD
∴两三角形相似比K=1:2,
∴ =K2= ,
则4(S△ABD-6)=S△ABD,
解得:S△ABD=8.
【解析】分析:(1)根据等腰三角形性质推出F为AD中点,根据三角形的中位线定理推出即可;(2)根据三角形中位线推出EF∥BD , 推出△AEF∽△ABD且两三角形相似比K=1:2,得出面积比是 ![]() ,代入求出即可.
,代入求出即可.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目