题目内容
如图,在平行四边形ABCD中,AB在x轴上,D点y轴上,∠C=60°,BC=6,B点坐标为(4,0).点M是边AD上一点,且DM:AD=1:3.点E、F分别从A、C同时出发,以1厘米/秒的速度分别沿AB、CB向点B运动(当点F运动到点B时,点E随之停止运动),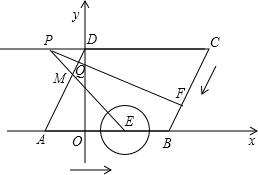 EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为
EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为| 5 | 2 |
(1)求直线BC的解析式;
(2)当x为何值时,PF⊥AD;
(3)在(2)问条件下,⊙E与直线PF是否相切?如果相切,加以证明,并求出切点的坐标;如果不相切,说明理由.
分析:(1)已知BC=6,点B的坐标为(4,0),可求出点C的坐标.设直线BC的解析式为y=kx+b,把已知坐标代入可求.
(2)如果PF⊥AD,那么PF与BC也垂直,由此可得出∠CPF=30°,即CF=
PC,可用x表示出CF、PC,根据CF,PC的比例关系式可得出关于x的方程,即可求出x的值.
(3)本题只要证E到PF的距离是否为
即可.过E作PF的垂线,设垂足为G,延长PF交x轴于M,过P作PN∥DA交x轴于N,由于PN∥AD,AD⊥PF,因此NP⊥PF,在直角三角形PNM中,∠PMN=30°,因此NG=2PN=12,那么EM=12-PD-AE=12-
-
=5,那么在直角三角形EGM中,∠PMN=30°,EM=5,因此EG=2.5=r,由此可得出PF与⊙E相切.
求切点即G点坐标时,可过G作x轴的垂线,即可通过构建的直角三角形,用三角形函数求出G点横坐标和纵坐标,进而可求出切点的坐标.
(2)如果PF⊥AD,那么PF与BC也垂直,由此可得出∠CPF=30°,即CF=
| 1 |
| 2 |
(3)本题只要证E到PF的距离是否为
| 5 |
| 2 |
| 14 |
| 6 |
| 14 |
| 3 |
求切点即G点坐标时,可过G作x轴的垂线,即可通过构建的直角三角形,用三角形函数求出G点横坐标和纵坐标,进而可求出切点的坐标.
解答: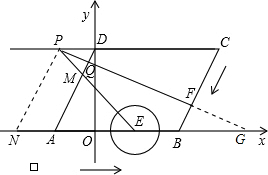 解:(1)y=
解:(1)y=
x-4
.
(2)∵PF⊥AD,AD∥BC
∴PF⊥BC
∵∠C=60°,
∴∠CPF=30°
∴CF=
PC,
又∵△PDM∽△EAM,且DM:AD=1:3,
∴PD:AE=1:2,
又∵AE=x,
∴PD=
x,
∵DC=AB=OA+OB=3+4=7,
∴PC=
x+7,
又∵CF=x,
∴x=
(
x+7)
∴x=
∵0<
<6
∴当x=
时,PF⊥AD.
(3)相切,
过E作PF的垂线,设垂足为G,延长PF交x轴于M,过P作PN∥DA交x轴于N,由于PN∥AD,AD⊥PF,因此NP⊥PF,在直角三角形PNM中,∠PMN=30°,因此MN=2PN=12,那么EM=12-PD-AE=12-
-
=5,那么在直角三角形EGM中,∠PMN=30°,EM=5,因此EG=2.5=r,由此可得出PF与⊙E相切.
求切点即G点坐标时,可过G作x轴的垂线GR⊥BE,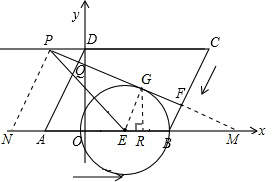
∵∠C=∠DAO=60°,BC=AD=6,
∴AO=3,
∴OE=
-3=
,
∵EG⊥PF,
∴AD∥GE∥BC,
∴∠GER=60°,
∴ER=
EG=
,
∴GR=
,
∴OR=
+
=
,
∴切点G的坐标为(
,
).
 解:(1)y=
解:(1)y=| 3 |
| 3 |
(2)∵PF⊥AD,AD∥BC
∴PF⊥BC
∵∠C=60°,
∴∠CPF=30°
∴CF=
| 1 |
| 2 |
又∵△PDM∽△EAM,且DM:AD=1:3,
∴PD:AE=1:2,
又∵AE=x,
∴PD=
| 1 |
| 2 |
∵DC=AB=OA+OB=3+4=7,
∴PC=
| 1 |
| 2 |
又∵CF=x,
∴x=
| 1 |
| 2 |
| 1 |
| 2 |
∴x=
| 14 |
| 3 |
∵0<
| 14 |
| 3 |
∴当x=
| 14 |
| 3 |
(3)相切,
过E作PF的垂线,设垂足为G,延长PF交x轴于M,过P作PN∥DA交x轴于N,由于PN∥AD,AD⊥PF,因此NP⊥PF,在直角三角形PNM中,∠PMN=30°,因此MN=2PN=12,那么EM=12-PD-AE=12-
| 14 |
| 6 |
| 14 |
| 3 |
求切点即G点坐标时,可过G作x轴的垂线GR⊥BE,

∵∠C=∠DAO=60°,BC=AD=6,
∴AO=3,
∴OE=
| 14 |
| 3 |
| 5 |
| 3 |
∵EG⊥PF,
∴AD∥GE∥BC,
∴∠GER=60°,
∴ER=
| 1 |
| 2 |
| 5 |
| 4 |
∴GR=
5
| ||
| 4 |
∴OR=
| 5 |
| 4 |
| 5 |
| 3 |
| 35 |
| 12 |
∴切点G的坐标为(
| 35 |
| 12 |
5
| ||
| 4 |
点评:本题主要考查了用待定系数法求一次函数的解析式,解直角三角形,相似三角形的判定和性质,切线的判定等知识点.
综合性较强,考查学生数形结合的数学思想方法.
综合性较强,考查学生数形结合的数学思想方法.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2| 2 |
| 3 |
| 5 |
| A、AC⊥BD |
| B、四边形ABCD是菱形 |
| C、△ABO≌△CBO |
| D、AC=BD |
 17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有
17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形. 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米. (2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为
(2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为