题目内容
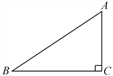
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)分别以直线AC,BC为轴,把△ABC旋转一周,得到两个不同的圆锥,求这两个圆锥的侧面积;
(2)以直线AB为轴,把△ABC旋转一周,求所得几何体的表面积.
【答案】(1) 80π;60π;(2)![]() .
.
【解析】(1)先利用勾股定理计算出AB=10,当以直线AC为轴,把△ABC旋转一周,得到的圆锥的底面半径是BC,母线长为AB,然后根据圆锥的侧面积公式计算;当以直线BC为轴,把△ABC旋转一周,得到的圆锥的底面半径为AC,母线长为AB, 然后根据圆锥的侧面积公式计算;
(2)作CD⊥AB于D,利用面积法可得到CD的长,由于以直线AB为轴,把△ABC旋转一周,所得几何体的是以CD为底面半径的两个圆锥,它的表面积就是两个圆锥的侧面积, 圆锥的侧面积公式计算.
(1)∵∠C=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
∴以直线AC为轴,把△ABC旋转一周,得到的圆锥的侧面积=π×8×10=80π;
以直线BC为轴,把△ABC旋转一周,得到的圆锥的侧面积=π×6×10=60π;
(2)如答图,过点C作CD⊥AB于点D.
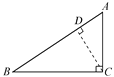
∵CD·AB=AC·BC,
∴CD=![]() =
=![]() ,
,
以直线AB为轴,把△ABC旋转一周,所得几何体是由以CD为底面半径的两个圆锥组成,则它的表面积=π×![]() ×6+π×
×6+π×![]() ×8=
×8=![]() π.
π.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目