��Ŀ����
����Ŀ�������龳:��ֱ��AB��һ��OΪ�˵�������OM��ON����һ��ֱ�������ε�ֱ�Ƕ������O��(��COD=90��).
(1)��ͼ1��ֱ�����ǰ�COD�ı�OD��������OB�ϣ�OMƽ�֡�AOC��ON��OB�غϣ����MON=_����
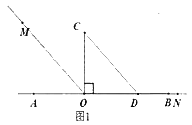
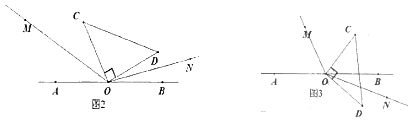
(2)ֱ�����ǰ�COD�Ƶ�O��ת����ͼ2��λ�ã�OMƽ�֡�AOC��ONƽ�֡�BOD�����MON�Ķ�����
(3)ֱ�����ǰ�COD�Ƶ�O��ת����ͼ3��λ�ã�OMƽ�֡� AOC ��ONƽ�֡�BOD�������MON�Ķ�������˵�����ɡ�
���𰸡���1��135��
��2����MON=135��
��3��������MON=135����֤��������.
��������
��1���������COM=45������������MON=��COM+��CON���������
��2���������AOC+��BOD=90�����ٸ���OMƽ����AOC��ONƽ����BOD����֪��COM+��DON=45������������MON=��COM+��DON+��COD���������
��3����ͼ�ӳ�NO��Q��DO��H������DOHΪƽ�ǣ���COH=90�������ݶԶ�����ȣ�֪��BOD=��AOH����NOD=��QOH���ٸ��ݡ�COH=��AOC-��AOH=90������OMƽ����AOC��ONƽ����BOD������COM-��QOH=45��������MON=��COD-��NOD+��COM=��COD+��COM-��QOH=90��+45��=135��.
��1���ߡ�AOC=90����OMƽ�֡�AOC��
����COM=45����
����MON=��COM+��CON=45��+90��=135����
��2���ߡ�COD=90����
����AOC+��BOD=90����
��OMƽ����AOC��ONƽ����BOD��
����COM+��DON=![]() ����AOC+��BOD��=45����
����AOC+��BOD��=45����
����MON=��COM+��DON+��COD=45��+90��=135����
��3��������MON=135����֤�����£�
��ͼ�ӳ�NO��Q��DO��H��
����DOHΪƽ�ǣ���COH=90����
���COH=��AOC-��AOH=90����
���ߡ�BOD=��AOH����NOD=��QOH��
OMƽ����AOC��ONƽ����BOD��
����COM-��QOH=45����
����MON=��COD-��NOD+��COM
=��COD+��COM-��QOH
=90��+45��=135��.