题目内容
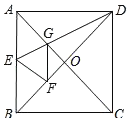
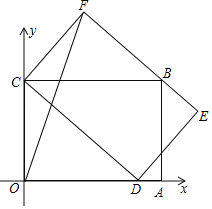
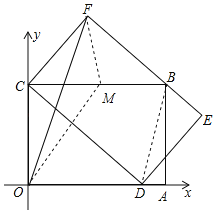
【题目】如图,矩形OABC的边OC在y轴上,边OA在x轴上,C点坐标为(0,3),点D是线段OA的一个动点,连接CD,以CD为边作矩形CDEF,使边EF过点B,已知所作矩形CDEF的面积为12,连接OF,则在点D的运动过程中,线段OF的最大值为__.
【答案】![]() .
.
【解析】
连接BD,由矩形的性质得出S矩形CDEF=2S△CBD=12,S矩形OABC=2S△CBD,得出S矩形OABC=12,可求OA=4=BC,由∠CFB=90°,C、B均为定点,F可以看作是在以BC为直径的圆上,取BC的中点M,则OF的最大值=OM+![]() BC=
BC=![]() .
.
连接BD,取BC中点M,连接OM,FM,
∵S矩形CDEF=2S△CBD=12,S矩形OABC=2S△CBD,
∴S矩形OABC=12,
∵C点坐标为(0,3),
∴OC=3,
∴BC=4,
∵∠CFB=90°,C、B均为定点,
∴F可以看作是在以BC为直径的圆上,且点M是BC中点,
则MF=![]() BC=CM=2,OM
BC=CM=2,OM![]() =
=![]() ,
,
当点O,点F,点M三点共线时,OF的值最大.
∴OF的最大值=OM+![]() BC=
BC=![]() ,
,
故答案为:![]()

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目