题目内容
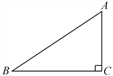
【题目】如图是一个水坝的横断面，坝顶宽CD＝8米，坝高DE＝12米，迎水坡BC的坡比i1＝1∶2，背水坡AD的坡比i2＝1∶1.
求：(1)∠A的度数；
(2)坝底宽AB.
【答案】(1) 45°；(2)44米.
【解析】（1）根据已知背水坡的坡度i2可求得∠A的度数；
（2）过点C作CF⊥AB于F，从而得到DC=EF，DE=CF，再根据坡度求得BF的长，这样就不难求出AB的长．
(1)∵tanA＝
，
∴AE＝DE，
∴∠A＝45°；
(2)如图，过点C作CF⊥AB于点F.
∵DE⊥AE，DC∥AB，
∴四边形EFCD为矩形，
∴DE＝CF＝12米，CD＝EF＝8米．
∵tanB＝
，∴BF＝2CF＝24米，
∴AB＝AE＋EF＋BF＝12＋8＋24＝44(米)．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
