题目内容
【题目】如图,在△ABC中,AD,BE分别为边BC,AC上的高线,D,E为垂足,M为AB的中点,N为DE的中点.求证:
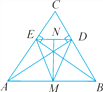
(1)△MDE是等腰三角形.
(2)MN⊥DE.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:
(1)AD,BE分别为边BC,AC上的高线,D,E为垂足,可得△ADB、△BEA是直角三角形,由M是AB边的中点,可得DM=EM=![]() AB,就可得△MDE是等腰三角形;
AB,就可得△MDE是等腰三角形;
(2)由△MDE是等腰三角形,N是底边DE的中点,可得MN⊥DE.
试题解析:
(1)∵AD,BE分别为边BC,AC上的高线,
∴△ABD,△ABE均为Rt△.
∵M是Rt△ABD斜边AB的中点,
∴MD=![]() AB.
AB.
同理,ME=![]() AB.
AB.
∴ME=MD.
∴△MDE是等腰三角形.
(2)∵在△MDE中,ME=MD,N是DE的中点,
∴MN⊥DE.

练习册系列答案
相关题目