题目内容
【题目】如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为 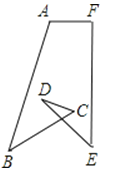
【答案】360°
【解析】解:如图连接BE.
∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,
∴∠C+∠D=∠CBE+∠DEB,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F.
又∵∠A+∠ABE+∠BEF+∠F=360°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.
所以答案是:360°.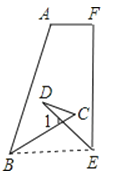
【考点精析】根据题目的已知条件,利用多边形内角与外角的相关知识可以得到问题的答案,需要掌握多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°.

练习册系列答案
相关题目