Question

【题目】如图，已知直线AB和CD相交于点O，∠COE=90°，OF平分∠AOE，∠COF=24°，求∠BOD的度数．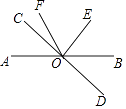

Answer 1

【答案】解：∵∠COF=24°，∠COE=90°， ∴∠EOF=∠COE﹣∠COF=90°﹣24°=66°，
∵OF平分∠AOE，
∴∠AOE=2∠EOF=66°×2=132°，
∴∠BOE=180°﹣132°=48°，
∵∠BOD=∠DOE﹣∠BOE=90°﹣48°=42°
【解析】直接利用角平分线的性质得出∠AOE的度数，进而得出∠BOE的度数，即可得出答案．
【考点精析】本题主要考查了角的平分线和对顶角和邻补角的相关知识点，需要掌握从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线；两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个才能正确解答此题．