题目内容
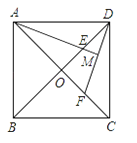
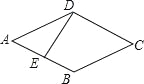
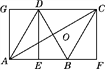
【题目】如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于D,交AF于B,交AC于O.连接AD,BC.
(1)求证:四边形ABCD是菱形;
(2)若E为AB的中点,DE⊥AB,求∠BDC的度数;
(3)在(2)的条件下,若AB=1,求菱形ABCD的对角线AC,BD的长.
【答案】(1)见解析;(2)60°;(3)BD=1,AC=![]()
【解析】试题分析: ![]() 根据垂直平分线的性质,可以得到
根据垂直平分线的性质,可以得到![]() 由矩形的性质,得到
由矩形的性质,得到![]() 根据平行线的性质,利用
根据平行线的性质,利用![]() 证明
证明![]() 从而得到
从而得到![]() ,结合上步所求,由四边相等的四边形是菱形即可得出结论.
,结合上步所求,由四边相等的四边形是菱形即可得出结论.
![]() 由题意,可以得到
由题意,可以得到![]() 垂直平分
垂直平分![]() 从而得出
从而得出![]() 结合题意可得
结合题意可得![]() 的度数,进而求得
的度数,进而求得![]() 的度数;
的度数;
![]() 根据菱形的性质,得到
根据菱形的性质,得到![]() 由此在
由此在![]() 中,求得
中,求得![]() 的值,进而可得
的值,进而可得![]() 的值.
的值.
试题解析: ![]()
![]() 垂直平分
垂直平分![]()
![]()
∵四边形![]() 是矩形,
是矩形,
![]()
![]()
![]()
![]()
![]()
∴四边形![]() 是菱形.
是菱形.
![]()
![]() 为
为![]() 的中点,
的中点, ![]()
![]() 垂直平分
垂直平分![]()
![]()
又![]()
![]() 为等边三角形,
为等边三角形,
![]()
![]()
![]()
![]() 由菱形性质知,
由菱形性质知, ![]()
在![]() 中,
中, ![]()
![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目