题目内容
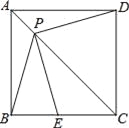
【题目】如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.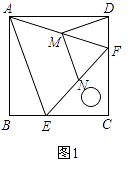
(1)尝试探究:
结论1:DM、MN的数量关系是;
结论2:DM、MN的位置关系是;
(2)猜想论证:证明你的结论.
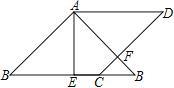
(3)拓展:如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,(1)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.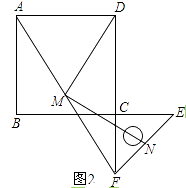
【答案】
(1)DM=MN;DM⊥MN
(2)
解:结论1:DM=MN,理由是:
如图1,∵M是AF的中点,N是EF的中点,
∴MN= ![]() AE,
AE,
∵四边形ABCD是正方形,
∴∠ADF=∠B=90°,AB=AD=BC=CD,
∴DM= ![]() AF,
AF,
∵△ECF是等腰直角三角形,
∴EC=FC,
∴BE=DF,
在△ABE和△ADF中,
∵  ,
,
∴△ABE≌△ADF(SAS),
∴AE=AF,
∴DM=MN;
结论2,DM、MN的位置关系是:DM⊥MN,理由是:
如图1,∵M是AF的中点,N是EF的中点,
∴MN∥AE,
∴∠NMF=∠EAF,
∵△ABE≌△ADF,
∴∠BAE=∠FAD,
Rt△ADF中,∵M是AF的中点,
∴AM=DM,
∴∠FAD=∠MDA,
∵∠FMD=∠FAD+∠MDA=∠FAD+∠BAE,
∴∠DMN=∠NMF+∠FMD=∠EAF+∠BAE+∠FAD=90°,
∴DM⊥MN
(3)
解:(2)中的两个结论还成立,
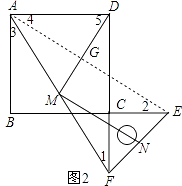
证明:连接AE,交MD于点G,
∵点M为AF的中点,点N为EF的中点,
∴MN∥AE,MN= ![]() AE,
AE,
由(1)同理可证,
AB=AD=BC=CD,∠B=∠ADF,CE=CF,
又∵BC+CE=CD+CF,即BE=DF,
∴△ABE≌△ADF,
∴AE=AF,
在Rt△ADF中,
∵点M为AF的中点,
∴DM= ![]() AF,
AF,
∴DM=MN,
∵△ABE≌△ADF,
∴∠1=∠2,
∵AB∥DF,
∴∠1=∠3,
同理可证:∠2=∠4,
∴∠3=∠4,
∵DM=AM,
∴∠MAD=∠5,
∴∠DGE=∠5+∠4=∠MAD+∠3=90°,
∵MN∥AE,
∴∠DMN=∠DGE=90°,
∴DM⊥MN.
【解析】解:(1)结论1:DM、MN的数量关系是:DM=MN,
结论2:DM、MN的位置关系是:DM⊥MN,
所以答案是:DM=MN,DM⊥MN;
【考点精析】本题主要考查了直角三角形斜边上的中线和三角形中位线定理的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案