题目内容
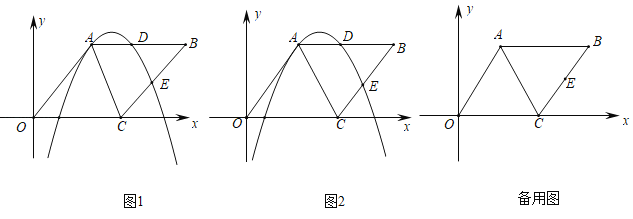
【题目】已知抛物线y=ax2+bx+3经过A(3,0),B(1,0)两点(如图1),顶点为M.
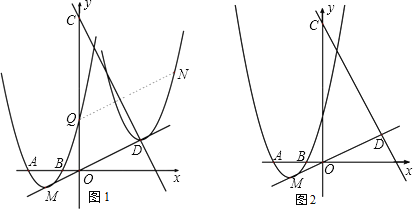
(1)a、b的值;
(2)设抛物线与y轴的交点为Q(如图1),直线y=2x+9与直线OM交于点D. 现将抛物线平移,保持顶点在直线OD上.当抛物线的顶点平移到D点时,Q点移至N点,求抛物线上的两点M、Q间所夹的曲线MQ扫过的区域的面积;
(3)设直线y=2x+9与y轴交于点C,与直线OM交于点D(如图2).现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)没有公共点时,试探求其顶点的横坐标h的取值范围.
【答案】(1)a=1,b=4;(2)MQ扫过的面积为![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)将A、B两点的坐标代入抛物线的解析式中,即可求出待定系数的值.
(2)连接MQ、DN后,由图可以发现曲线MQ扫过的面积正好是MQND的面积;连接QD,则MQND的面积是两倍的△MQD的面积,所以这道题实际求的是△MQD的面积;由(1)的抛物线解析式,不难求出顶点M的坐标,联立直线OM和直线CD的解析式可以求出点D的坐标;以OQ为底,M、D两点的横坐标差的绝对值为高即可得△MQD的面积,则此题可求.
(3)在平移过程中,抛物线的开口方向和大小是不变的,即二次项系数不变;抛物线的顶点始终在直线OM上,根据直线OM的解析式(y=![]() x)可表达出抛物线顶点的坐标(h,
x)可表达出抛物线顶点的坐标(h,![]() h),可据此先设出平移后的抛物线解析式;若求平移的抛物线与射线CD(含端点C)没有公共点时顶点横坐标的取值范围,那么就要考虑到两个关键位置:
h),可据此先设出平移后的抛物线解析式;若求平移的抛物线与射线CD(含端点C)没有公共点时顶点横坐标的取值范围,那么就要考虑到两个关键位置:
①抛物线对称轴右侧部分经过C点时,抛物线顶点横坐标h的值;
②抛物线对称轴左侧部分与直线CD恰好有且只有一个交点时,h的值;
解:(1)将A(-3,0),B(-1,0)代入抛物线y=ax2+bx+3中,得:
![]() ,
,
解得:a=1、b=4.
(2)连接MQ、QD、DN,
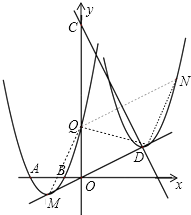
由图形平移的性质知:QN∥MD,即四边形MQND是平行四边形;
由(1)知,抛物线的解析式:y=x2+4x+3=(x+2)2-1,则点M(-2,-1),
当x=0时,y=3,
∴Q(0,3);
设直线OM的解析式为y=kx,
∴-2k=-1,
∴k=![]() ,
,
∴直线OM:y=![]() x,联立直线y=-2x+9,得:
x,联立直线y=-2x+9,得:
 ,
,
解得
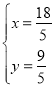 .
.
则D(![]() );
);
曲线QM扫过的区域的面积:S=S![]() MQND=2S△MQD
MQND=2S△MQD![]() ;
;
(3)由于抛物线的顶点始终在y=![]() x上,可设其坐标为(h,
x上,可设其坐标为(h,![]() h),设平移后的抛物线解析式为y=
h),设平移后的抛物线解析式为y=![]() h;
h;
①当平移后抛物线对称轴右侧部分经过点C(0,9)时,有:
h2+![]() h=9,解得:h=
h=9,解得:h=![]() (依题意,舍去正值)
(依题意,舍去正值)
②当平移后的抛物线与直线y=-2x+9只有一个交点时,依题意:
 ,
,
消去y,得:x2-(2h-2)x+h2+![]() h-9=0,
h-9=0,
则:△=(2h-2)2-4(h2+![]() h-9)=-10h+40=0,解得:h=4,
h-9)=-10h+40=0,解得:h=4,
结合图形,当平移的抛物线与射线CD(含端点C)没有公共点时,h<![]() 或h>4.
或h>4.