题目内容
【题目】如图.在平行四边形![]() 中,分
中,分![]() 别为
别为![]() 的中点,连结
的中点,连结![]() .
.
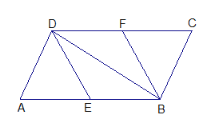
求证:
(1)![]() ;
;
(2)若![]() ,证明:四边形
,证明:四边形![]() 是菱形。
是菱形。
【答案】(1)见解析;(2)见解析
【解析】
(1)根据平行四边形的性质可得AD=BC,∠A=∠C,DC=AB,再结合条件可得AE=CF,再利用SAS证明△ADE≌△CBF即可;
(2)首先利用平行四边形的性质证明DF∥EB,DF=EB,可得四边形DEBF是平行四边形,再利用直角三角形的性质可得DE=![]() AB,进而可得DE=EB,从而可证明四边形
AB,进而可得DE=EB,从而可证明四边形![]() 是菱形.
是菱形.
证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,DC=AB,
∵E,F分别为边AB、CD的中点,
∴DF=CF=![]() DC,AE=BE=
DC,AE=BE=![]() AB,
AB,
∴AE=CF,
在△ADE和△CBF中
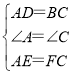 ,
,
∴△ADE≌△CBF(SAS);
![]()
(2)∵边形ABCD是平行四边形,
∴DC=AB,CD∥AB,
∴DF∥EB,
∵E,F分别为边AB、CD的中点,
∴DF=CF=![]() DC,AE=BE=
DC,AE=BE=![]() AB,
AB,
∴DF=EB,
∴四边形DEBF是平行四边形,
∵∠ADB=90°,
∴DE=![]() AB,
AB,
∴DE=EB,
∴四边形DEBF是菱形.

练习册系列答案
相关题目