��Ŀ����
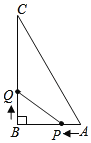
����Ŀ����ͼ������ABC�У���B��90����AB��6cm��BC��8cm����P��A�㿪ʼ��AB�����B��1cm/����ٶ��ƶ���ͬʱ��Q��B�㿪ʼ��BC�����C��2cm/����ٶ��ƶ����ҵ�����һ�㵽���յ�ʱ����һ������ֹ֮ͣ�ƶ���
��1��P��Q������������ʹ��PBQ�����Ϊ8cm2��
��2����P��Q����ͬʱ�����ƶ���ʱ��Ϊt�룬��PBQ�����ΪScm2����д��S��t�ĺ�����ϵʽ���������PBQ��������ֵ��
���𰸡���1������2��4�����PBQ���������8cm2����2�����ƶ������У���PBQ����������9cm2��
��������
��1�������⣬����P��Q����t�룬ʹ��PBQ�����Ϊ8cm2����PB=6-t��BQ=2t����������������ļ��㹫ʽ��S��PBQ=![]() BP��BQ���г�����ʽ���������ɣ�
BP��BQ���г�����ʽ���������ɣ�
��2�������⣬����P��Q����t�룬��PB=6-t��BQ=2t����������������ļ��㹫ʽ��S��PBQ=![]() BP��BQ���г�����ʽ��Ȼ��������������ֵ����.
BP��BQ���г�����ʽ��Ȼ��������������ֵ����.
�⣺��1���辭��t���PBQ���������8cm2��
![]() ����6��t����2t��8��
����6��t����2t��8��
��ã�t1��2��t2��4��
�𣺾���2��4���PBQ���������8cm2��
��2�������⣬��S��![]() ��PB��BQ��
��PB��BQ��![]() ����6��t����2t����t2+6t������t��3��2+9��
����6��t����2t����t2+6t������t��3��2+9��
�����ƶ������У���PBQ����������9cm2��

����Ŀ��ij�̳��ƻ�����A��B�������ͽ���̨�ƹ�50յ��������̨�ƵĽ��ۡ��ۼ����±���ʾ��
A�� | B�� | |
���ۣ�Ԫ/յ�� | 40 | 65 |
�ۼۣ�Ԫ/յ�� | 60 | 100 |
��1�������̳���������̨�ƹ���ȥ2500Ԫ����������̨�Ƹ���������յ��
��2����ÿ��̨���������������£������̳���������̨�Ƶ�����������1400Ԫ���������蹺��B��̨�ƶ���յ��
��3�������̳�Ԥ���ò�����2500Ԫ�Ҳ�����2600Ԫ���ʽ�����̨�ƣ�Ϊ�˴�B��̨�Ƶ���·���̳�����ÿ�۳�һյB��̨�ƣ������˿��ֽ�aԪ��10��a��20�����ʸ��̳�����ν��������ܻ����������