��Ŀ����
����Ŀ�����壺һ�����ε����ڱ�֮��Ϊ ![]() ����Ƹþ���Ϊ���رȾ��Ρ���
����Ƹþ���Ϊ���رȾ��Ρ���
��1����ͼ�٣��ڡ��رȾ��Ρ�ABCD�У� ![]() =
= ![]() �����AOD�Ķ�����
�����AOD�Ķ����� 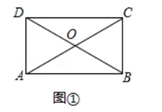
��2����ͼ�ڣ��رȾ���CDEF�ı�CD�ڰ�ԲO��ֱ��AB�ϣ�����E��F�ڰ�Բ�ϣ���ֱ֪��AB= ![]() �������CDEF�������
�������CDEF������� 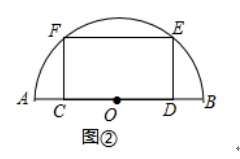
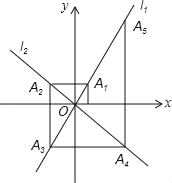
��3����ƽ��ֱ������ϵxOy�У���O�İ뾶Ϊ ![]() ����Q������Ϊ��q��2
����Q������Ϊ��q��2 ![]() ��������ڡ�O�ϴ���һ��P������P��x��Ĵ��������Q��y��Ĵ��߽��ڵ�M������P��y��Ĵ��������Q��x��Ĵ��߽��ڵ�N���Ե�P��Q��M��NΪ����ľ����ǡ��رȾ��Ρ�����ֱ��д��q��ȡֵ��Χ��
��������ڡ�O�ϴ���һ��P������P��x��Ĵ��������Q��y��Ĵ��߽��ڵ�M������P��y��Ĵ��������Q��x��Ĵ��߽��ڵ�N���Ե�P��Q��M��NΪ����ľ����ǡ��رȾ��Ρ�����ֱ��д��q��ȡֵ��Χ�� 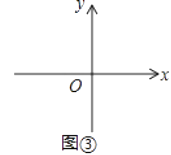
���𰸡�
��1���⣺��ͼ���У�
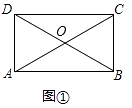
���ı���ABCD�Ǿ��Σ�
���ABC=90�㣬OA=OC=OD=OB��
��tan��ACB= ![]() =
= ![]() ��
��
���ACB=60�㣬��OC=OB��
���OBC�ǵȱ������Σ�
���AOD=��BOC=60�㣮
��2���⣺��ͼ���У�����OE����DE=a����CD= ![]() a��
a��

��CF=DE��OE=OF����FCO=��EDO=90�㣬
��Rt��FOC��Rt��EDO��
��OC=OD= ![]() a��
a��
��Rt��OED��OE= ![]() ��
��
��OE2=DE2+OD2��
�� ![]() =a2+
=a2+ ![]() a2��
a2��
��a=1�������Ѿ���������
��DE=1��CD= ![]() ��
��
�����CDEF�����=1�� ![]() =
= ![]() ��
��
��3���⣺��ͼ���У�

�ٵ���P��x���������ϣ���֪PM=2 ![]() ��
��
���ı���PMQN�ǡ��رȾ��Ρ���
��MQ= ![]() PM=6����ʱQ��
PM=6����ʱQ�� ![]() +6��2
+6��2 ![]() ����
����
����P����y�����������ʱ��P��M��= ![]() ��
��
���ı���PMQN�ǡ��رȾ��Ρ���
��P��M��= ![]() M��Q�䣬
M��Q�䣬
��M��Q��=1��
��Q�䣨1��2 ![]() ����
����
���ݶԳ��ԡ��۲�ͼ���֪����Q�ĺ�����q��ȡֵ��ΧΪ1�ܡ� ![]() +6��
+6�� ![]() ��6��q�ܩ�1��
��6��q�ܩ�1��
����������1����tan��ACB= ![]() =
= ![]() ���Ƴ���ACB=60�㣬��OC=OB���Ƴ���OBC�ǵȱ������μ��ɽ�����⣮��2����ͼ���У�����OE����DE=a����CD=
���Ƴ���ACB=60�㣬��OC=OB���Ƴ���OBC�ǵȱ������μ��ɽ�����⣮��2����ͼ���У�����OE����DE=a����CD= ![]() a����Rt��FOC��Rt��EDO���Ƴ�OC=OD=
a����Rt��FOC��Rt��EDO���Ƴ�OC=OD= ![]() a����Rt��OED�У�OE=
a����Rt��OED�У�OE= ![]() ������OE2=DE2+OD2 �� �г����̼��ɽ�����⣮��3��ȡ��������㣬�����Q�����꣬�ٸ��ݶԳ��Լ��ɽ�����⣮
������OE2=DE2+OD2 �� �г����̼��ɽ�����⣮��3��ȡ��������㣬�����Q�����꣬�ٸ��ݶԳ��Լ��ɽ�����⣮