题目内容
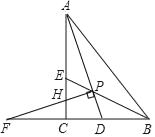
【题目】如图(1),在平面直角坐标系中,直线y=﹣![]() x+4交坐标轴于A、B两点,过点C(﹣4,0)作CD⊥AB于D,交y轴于点E.
x+4交坐标轴于A、B两点,过点C(﹣4,0)作CD⊥AB于D,交y轴于点E.
(1)求证:△COE≌△BOA;
(2)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①判断△OMN的形状.并证明;
②当△OCM和△OAN面积相等时,求点N的坐标.

【答案】(1)证明见解析;(2)①△MON是等腰直角三角形;②点N的坐标为(1.5,2).
【解析】
(1)代入解析式后得出OB,OA的长,再利用全等三角形的判定证明即可;
(2)①根据全等三角形的判定和性质得出OM=ON,再利用等腰直角三角形的判定解答即可;
②根据全等三角形的性质和三角形面积公式解答即可.
解:(1)把x=0代入y=﹣![]() x+4,
x+4,
解得:y=4,
∴OB=4,
把y=0代入y=﹣![]() x+4,解得:x=3,
x+4,解得:x=3,
∴OA=3,
∵C(﹣4,0),
∴OC=4,
∴OB=OC,
∵CD⊥AB,
∴∠ACD+∠CAD=90°,
∵∠ACD+∠OEC=90°,
∴∠CAD=∠OEC,
在△COE与△BOA中
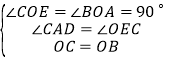 ,
,
∴△COE≌△BOA(AAS);
(2)①∵ON⊥OM,
∴∠MON=90°,
∴∠COM+∠AON=90°,
∵∠AON+∠BON=90°,
∴∠COM=∠BON,
∵△COE≌△BOA,
∴∠OCM=∠OBN,
在△COM与△BON中
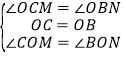 ,
,
∴△COM≌△BON(ASA),
∴OM=ON,∠COM=∠BON,
∵∠COM+∠MOE=90°,
∴∠BON+∠MOE=90°,
即∠MON=90°,
∴△MON是等腰直角三角形;
②∵△COM≌△BON,△OCM与△OAN面积相等,
∴△BON与△OAN面积相等,
即△OAN面积是△AOB面积的一半,
![]() ,
,
解得:![]() =2,
=2,
把y=2代入y=﹣![]() x+4,
x+4,
解得:x=1.5,
∴点N的坐标为(1.5,2).