��Ŀ����
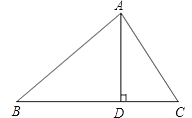
����Ŀ����ͼ1��D��BC�е㣬AD��BC��E��BC�ϳ�B��D��C������һ�㣬������SAS������֤��![]() ������AB��AC����B����C������ABE����ACE�У�
������AB��AC����B����C������ABE����ACE�У�![]() ������֤��
������֤��![]() ����Ϊ������SSA�������Σ�
����Ϊ������SSA�������Σ�![]() �Ƕ۽������Σ�
�Ƕ۽������Σ�![]() ����������Σ����Dz�����ȫ�ȣ�������������ζ���ֱ�������Σ���SSA���ͱ����HL�����Ϳ�������֤������������ȫ�ȣ�ͬ�����������֪�����������ζ��Ƕ۽������λ���������Σ���������������SSA�������Σ�Ҳ��һ����ȫ�ȵģ�������ͨ������ֱ�������������֤����
����������Σ����Dz�����ȫ�ȣ�������������ζ���ֱ�������Σ���SSA���ͱ����HL�����Ϳ�������֤������������ȫ�ȣ�ͬ�����������֪�����������ζ��Ƕ۽������λ���������Σ���������������SSA�������Σ�Ҳ��һ����ȫ�ȵģ�������ͨ������ֱ�������������֤����
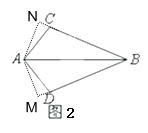
���⣺��֪����ͼ2��AD��AC��![]() ��
��
��1��������������ֱ��֤��![]() ��������?Ϊʲô?
��������?Ϊʲô?
��2����֤��![]() ��
��

���𰸡���1������������������ֱ��֤��![]() �����ɼ���������2��������.
�����ɼ���������2��������.
��������
��1�����ݱ߽߱Dz���֤������������ȫ�Ƚ��н��
��2����AN��BC��BC�ӳ�����N��AM��BD��BD�ӳ�����M���ɵá�M=��N=90����Ȼ������AAS֤����ACN����ADM���õ�AN=AM����Ϲ�����AB=AB������HL֤��Rt��ABN��Rt��ABM�������õ�![]() .
.
�⣺��1������������������ֱ��֤��![]() ����Ϊ�߽߱Dz���֤������������ȫ�ȣ���Ҫ�ȹ���ֱ�������ν���֤����
����Ϊ�߽߱Dz���֤������������ȫ�ȣ���Ҫ�ȹ���ֱ�������ν���֤����
��2����ͼ����AN��BC��BC�ӳ�����N��AM��BD��BD�ӳ�����M��
���M=��N=90����
��![]() ��
��
���ACN=��ADM��
�֡�AD��AC��
����ACN����ADM��AAS����
��AN=AM��
�֡�AB=AB��
��Rt��ABN��Rt��ABM��HL����
��![]() .
.

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�