Question

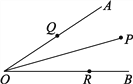
【题目】如图，∠AOB＝30°，角内有一点P，PO＝10cm，两边上各有一点Q，R(均不同于点O)，则△PQR的周长的最小值是多少？

Answer 1

【答案】10cm

【解析】试题分析：设点P关于OA的对称点是E，关于OB的对称点是F，当点R、Q在EF上时，△PQR的周长=PQ+QR+PR=EF，此时周长最小．

试题解析：作出点P关于OA的对称点E，作出点P关于OB的对称点F，连接EF，交OA于Q，交OB于R．连接PQ，PR，PE，PF，OE，OF，

则PQ=EQ，PR=RF，

则△PQR的周长=PQ+QR+PR=EQ+QR+RF=EF，

∵∠AOP=∠AOE，∠POB=∠FOB，∠AOB=∠AOP+∠POB=30°，

∴∠EOF=90°，

又∵OE=OP，OF=OP，

∴OE=OF=10，

即△EOF是等边三角形，

∴EF=OP=10，

所以△PQR的周长的最小值为10．