题目内容
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(10,4),点D是OA的中点,点P在边BC上运动,当△ODP是等腰三角形时,点P的坐标为 . 
【答案】(2,4)或(3,4)或(8,4)或(2.5,4)
【解析】解:∵B的坐标是(10,4),四边形OCBA是矩形, ∴OC=AB=4,
∵D为OA中点,
∴OD=AD=5,
∵P在BC上,
∴P点的纵坐标是4,
以O为圆心,以OD为半径作弧,交BC于P,如图1所示: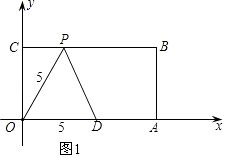
此时OP=OD=5,
由勾股定理得:CP=3,
即P的坐标是(3,4);
由勾股定理得:CP=3,
即P的坐标是(3,4);
以D为圆心,以OD为半径作弧,交BC于P、P′,如图2所示: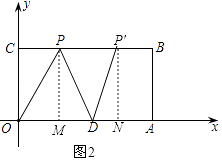
此时DP=OD=DP′=5,
由勾股定理得:DM=DN=3,
即P的坐标是(2,4),
P′的坐标是(8,4);
③作OD的垂直平分线交BC于P,如图3所示: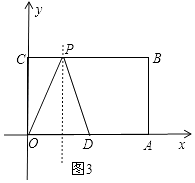
此时OP=DP,P的坐标是(2.5,4);
所以答案是:(2,4)或(3,4)或(8,4)或(2.5,4).
【考点精析】掌握等腰三角形的性质和矩形的性质是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目